科目：czsx 来源： 题型：

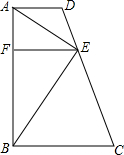（2013•大庆）如图所示，在直角梯形ABCD中，AB为垂直于底边的腰，AD=1，BC=2，AB=3，点E为CD上异于C，D的一个动点，过点E作AB的垂线，垂足为F，△ADE，△AEB，△BCE的面积分别为S₁，S₂，S₃．
（1）设AF=x，试用x表示S₁与S₃的乘积S₁S₃，并求S₁S₃的最大值；
（2）设

AF

FB

=t，试用t表示EF的长；
（3）在（2）的条件下，当t为何值时，S22=4S₁S₃．

科目：czsx 来源：2013年初中毕业升学考试（黑龙江大庆卷）数学（解析版） 题型：解答题

科目：czsx 来源：2013年黑龙江省大庆市中考数学试卷 （解析版） 题型：解答题

如图所示，在直角梯形ABCD中，AB为垂直于底边的腰，AD=1，BC=2，AB=3，点E为CD上异于C，D的一个动点，过点E作AB的垂线，垂足为F，△ADE，△AEB，△BCE的面积分别为S₁，S₂，S₃．
（1）设AF=x，试用x表示S₁与S₃的乘积S₁S₃，并求S₁S₃的最大值；
（2）设=t，试用t表示EF的长；
（3）在（2）的条件下，当t为何值时，=4S₁S₃．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：044

科目：czsx 来源：2009年江苏省无锡市江南中学中考数学二模试卷（解析版） 题型：填空题

科目：czsx 来源：2011年江苏省无锡市育才中学中考数学一模试卷（解析版） 题型：填空题

科目：czsx 来源： 题型：填空题

科目：czsx 来源： 题型：

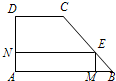20、如图，直角梯形ABCD中，∠A=90°，∠B=45°，底边AB=5，高AD=3，点E由B沿折线BCD向点D移动，EM⊥AB于M，EN⊥AD于N，设BM=x，矩形AMEN的面积为y，那么y与x之间的函数关系的图象大致是（　　）

A、

B、

C、

D、

科目：czsx 来源： 题型：

（2012•响水县一模）如图，在直角梯形ABCD中，AD∥BC，∠A=90°，BD⊥DC，BC=10cm，CD=6cm．在线段BC、CD上有动点F、E，点F以每秒2cm的速度，在线段BC上从点B向点C匀速运动；同时点E以每秒1cm的速度，在线段CD上从点C向点D匀速运动．当点F到达点C时，点E同时停止运动．设点F运动的时间为t（秒）．

（1）求AD的长；
（2）设四边形BFED的面积为y，求y 关于t的函数关系式，并写出函数自变量取值范围；
（3）点F、E在运动过程中，如△CEF与△BDC相似，求线段BF的长．
（4）以BF为半径的圆B与以DE为半径的圆D如果相切，直接写出t的值．

科目：czsx 来源： 题型：

如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
（1）当t为何值时，四边形PQDC的面积是梯形ABCD的面积的一半；
（2）四边形PQDC能为平行四边形吗？如果能，求出t的值；如果不能，请说明理由．
（3）四边形PQDC能为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由．

科目：czsx 来源： 题型：

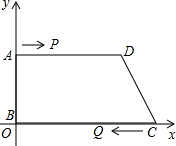在直角梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，建立如图所示的直角坐标系，动点P以1cm/s的速度由A沿AD向D运动；同时动点Q以3cm/s的速度由C沿CB向B运动，当其中一点到达端点时停止，另一点随之停止，设运动时间为t．
（1）t为何值时，四边形PQCD为平行四边形？
（2）求当四边形PQCD为平行四边形时，直线PQ的函数解析式；
（3）四边形PQCD能为等腰梯形吗？如果能，求出t值；若不能，请说明理由．

科目：czsx 来源： 题型：

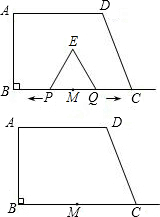如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=6，BC=8，AB=3

3

，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒（t＞0）．
（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）；
（2）当BP=1时，求△EPQ与梯形ABCD重叠部分的面积；
（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

科目：czsx 来源： 题型：

如图1，在直角梯形ABCD中，AD∥BC，∠A=90°，BD⊥DC，BC=10cm，CD=6cm．有两个动点E、F分别在线段CD与BC上运动，点E以每秒1cm的速度从点C向点D匀速运动．点F以每秒2cm的速度从点B向点C匀速运动；当其中一点到达终点时，另一点也随之停止．设运动的时间为t秒．
（1）求AD的长；
（2）设四边形BFED的面积为y，求y 关于t的函数关系式，并写出t的取值范围；
（3）点E、F在运动过程中，如果由点C、E、F构成的三角形与△BDC相似，求线段BF的长．

科目：czsx 来源： 题型：

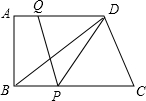
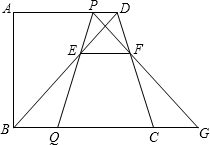如图，已知在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=11，BC=13，AB=12．动点P、Q分别在边AD和BC上，且BQ=2DP．线段PQ与BD相交于点E，过点E作EF∥BC，交CD于点F，射线PF交BC的延长线于点G，设DP=x．
（1）求

DF

CF

的值．
（2）当点P运动时，试探究四边形EFGQ的面积是否会发生变化？如果发生变化，请用x的代数式表示四边形EFGQ的面积S；如果不发生变化，请求出这个四边形的面积S．
（3）当△PQG是以线段PQ为腰的等腰三角形时，求x的值．

科目：czsx 来源： 题型：

如图1，在直角梯形ABCD中，AD∥BC，∠C=90°，BC=12，AD=18，AB=10．动点P、Q分别从点D、B同时出发，动点P沿射线DA的方向以每秒2个单位长的速度运动，动点Q在线段BC上以每秒1个单位长的速度向点C运动，当点Q运动到点C时，点P随之停止运动．设运动的时间为t（秒）．
（1）当点P在线段DA上运动时，连接BD，若∠ABP=∠ADB，求t的值；
（2）当点P在线段DA上运动时，若以BQ为直径的圆与以AP为直径的圆外切，求t的值；
（3）设射线PQ与射线AB相交于点E，△AEP能否为等腰三角形？如果能，请直接写出t的值；如果不能，请说明理由．

科目：czsx 来源： 题型：

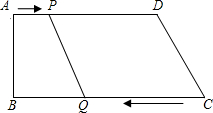如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AB=8厘米，AD=24厘米，BC=26厘米；点P从点A开始沿AD边向点D以1厘米/秒的速度移动，点Q从点C开始沿CB边向点B以3厘米/秒的速度移动；如果点P、Q分别从点A、C同时出发，当其中一点到达终点时，另一点也随之停止移动，设移动的时间为t秒．
（1）当t为何值时，四边形PQCD为平行四边形？
（2）当t为何值时，四边形PQCD的面积与四边形ABQP的面积相等？
（3）设四边形PQCD的面积为y，求y与t的函数关系式？探索四边形PQCD的面积是否存在最大值？若存在，最大值是多少？若不存在，说明理由？

科目：czsx 来源： 题型：

（2010•同安区质检）如图，在直角梯形ABCD中，∠A=90°，DC∥AB，CD=

1

2

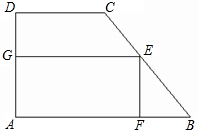AB=a，AD=3，E为线段BC上的动点（不与点B、点C重合），EF⊥AB于F，EG⊥AD于G，设EF=x，EG=y．
（1）求y关于x的函数关系式（系数可含a），并写出自变量x的取值范围；
（2）无论a为何正数，在点E运动的过程中，我们都可以看出y随着x的增大而减小．小明说此时四边形AFEG的周长w也是随着x的增大而减小．你认为他说的是否正确？如果正确，请说明理由；如果不正确，请举出反例．

科目：czsx 来源： 题型：

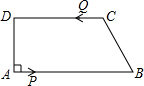如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，AB=20 cm，BC=10 cm，DC=12 cm，点P和Q同时从A、C出发，点P以4 cm/s的速度沿A-B一C-D运动，点Q从C开始沿CD边以1 cm/s的速度运动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s）．
（1）t为何值时，四边形APQD是矩形；
（2）t为何值时，四边形BCQP是等腰梯形；
（3）是否存在某一时刻t，使线段PQ恰好把梯形ABCD的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由．

科目：czsx 来源： 题型：

如图，在直角梯形ABCD中，AB∥CD，∠A=90°，AB=2，AD=5，P是AD上一动点（不与A、D重合），PE上BP，P为垂足，PE交DC于点E．
（1）△ABP和△DPE是否相似？请说明理由；
（2）设AP=x，DE=y，求y与x之间的函数关系式，并指出x的取值范围；
（3）请你探索在点P运动的过程中，四边形ABED能否构成矩形？如果能，求出AP的长；如果不能，请说明理由；
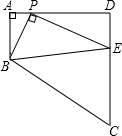（4）请你探索在点P的运动过程中，△BPE能否构成等腰三角形？如果能．求出AP的长；如果不能，请说明理由．