科目：czsx 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（解析版） 题型：解答题
已知：如图，在△ABC中，AB＝AC，∠A＝60°，BD是中线，延长BC至点E，使CE＝CD．
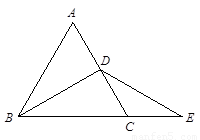
求证：DB＝DE．
科目：czsx 来源：2011年初中毕业升学考试（广西区北海卷）数学 题型：解答题
(10分)如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于
点D，过
点D作EF⊥AC于点E，交AB的延长线于点F．
(1)求证：EF是⊙O的切线；
(2)当∠B
AC＝60º时，DE与DF有何数量关系？请说明理由；
(3)当AB＝5，BC＝6时，求tan∠BAC的值．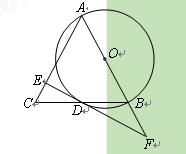
科目：czsx 来源： 题型：
(10分)如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过
点D作EF⊥AC于点E，交AB的延长线于点F．
(1)求证：EF是⊙O的切线；
(2)当∠BAC＝60º时，DE与DF有何数量关系？请说明理由；
(3)当AB＝5，BC＝6时，求tan∠BAC的值．
科目：czsx 来源：2013届江苏省阜宁县九年级第一次调研数学试卷（带解析） 题型：单选题
如图，在△ABC中，∠A＝70°，∠C＝60°，D、E分别是AB、AC上的点，且DE∥BC，则∠ADE的度数为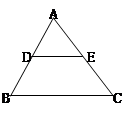
A．60° B．70° C．50° D．80°
科目：czsx 来源：2010年高级中等学校招生全国统一考试数学卷（辽宁丹东） 题型：选择题
如图，在△ABC中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是
A．40° B．60° C．70° D．80
科目：czsx 来源：2012届浙江天门市实验初级中学九年级三轮考试数学卷（一）（带解析） 题型：解答题
阅读下列材料，按要求解答问题：
如图2－1，在ΔABC中，∠A＝2∠B，且∠A＝60°．小明通过以下计算：由题意，∠B＝30°，∠C＝90°，c＝2b，a＝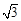
b，得a2－b2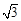＝(b)2－b2＝2b2＝b·c．即a2－b2＝ bc．
于是，小明猜测：对于任意的ΔABC，当∠A＝2∠B时，关系式a2－b2＝bc都成立．
（1）如图2－2，请你用以上小明的方法，对等腰直角三角形进行验证，判断小明的猜测是否正确，并写出验证过程；
（2）如图2－3，你认为小明的猜想是否正确，若认为正确，请你证明；否则，请说明理由；
（3）若一个三角形的三边长恰为三个连续偶数，且∠A＝2∠B，请直接写出这个三角形三边的长，不必说明理由．
科目：czsx 来源：2014届江苏省崇安区七年级下学期期中考试数学卷（解析版） 题型：选择题
如图，在△ABC中，∠A＝52°，∠ABC与∠ACB的角平分线交于D1， ∠ABD1与∠ACD1的角平分线交于点D2，依次类推，∠ABD4与∠ACD4 的角平分线交于点D5，则∠BD5C的度数是………………（ ）
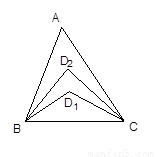
A．94° B．68° C．60° D．56°
科目：czsx 来源：2015届江苏泰州七年级下学期3月月考数学试卷（解析版） 题型：选择题
如图，在△ABC 中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是 （ ）
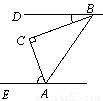
A．40° B．60° C．70° D．80°
科目：czsx 来源：2011-2012学年浙江省桐乡市学校九年级第一学期期末调研测试数学卷 题型：填空题
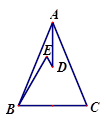
如图，在△ABC中，AB＝AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC＝∠E＝60º，若BE＝6 cm，DE＝2cm，则BC＝______________．
科目：czsx 来源： 题型：
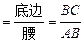．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
，试求sad A的值
|
 | |||
 | |||
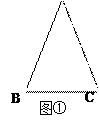科目：czsx 来源：2011～2012学年江苏省苏州工业园区九年级上学期期中测试数学卷 题型：解答题
(本题满分8分)通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图①在△ABC中，AB＝AC，顶角A的正对记作sad A，这时sad A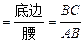
．容易知道一个角的大小与这个角的正对值也是相互
唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad 60°＝ ．
（2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是
（3）如图②，在Rt△ABC中，∠C＝90°，sin A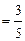
，试求sad A的值
|
 | |||
 | |||
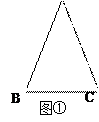科目：czsx 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（带解析） 题型：解答题
已知：如图，在△ABC中，AB＝AC，∠A＝60°，BD是中线，延长BC至点E，使CE＝CD．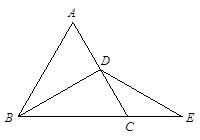
求证：DB＝DE．
科目：czsx 来源：2012-2013学年江苏泰州姜堰第四中学七年级下学期3月月考数学试卷（带解析） 题型：单选题
如图，在△ABC 中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是 （ ）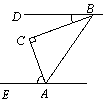
| A．40° | B．60° | C．70° | D．80° |
科目：czsx 来源：2011年初中毕业升学考试（广西柳州卷）数学 题型：解答题
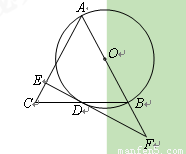
(10分)如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过
点D作EF⊥AC于点E，交AB的延长线于点F．
(1)求证：EF是⊙O的切线；
(2)当∠BAC＝60º时，DE与DF有何数量关系？请说明理由；
(3)当AB＝5，BC＝6时，求tan∠BAC的值．
科目：czsx 来源：2014届广西大学附属中学八年级11月段考数学试卷（解析版） 题型：解答题
如图，在ΔABC中，AB＝AC， AD＝AE，∠BAD＝60°,求∠EDC的度数。
科目：czsx 来源： 题型：
(本题满分8分)通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图①在△ABC中，AB＝AC，顶角A的正对记作sad A，这时sad A
．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad 60°＝ ．
（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是
（3）如图②，在Rt△ABC中，∠C＝90°，sin A
，试求sad A的值
|
| ||||||||
 | ||||||||
 | ||||||||
 | ||||||||
| ||||||||
科目：czsx 来源： 题型：
| A．94° | B．68° | C．60° | D．56° |
科目：czsx 来源：2011-2012学年湖北省武汉市车站中学八年级上学期期末数学试卷（带解析） 题型：解答题
如图，在△ABC中，AB＝AC，若将△ABC沿CA的方向平移CA的长，得△EFA，
⑴若△ABC的面积为3cm2，求四边形BCEF的面积
⑵试猜想AF与BE有何关系？
⑶若∠BAC＝60°，求∠FEB的度数。
科目：czsx 来源：2012年初中毕业升学考试（广西北海卷）数学（带解析） 题型：解答题
已知：如图，在△ABC中，∠A＝30°，∠B＝60°。
（1）作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作
法和证明）；
（2）连接DE，求证：△ADE≌△BDE。
科目：czsx 来源：2012届浙江省桐乡市河山镇中学学校九年级第一学期期末调研测试数学卷 题型：填空题
如图，在△ABC中，AB＝AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC＝∠E＝60º，若BE＝6 cm，DE＝2cm，则BC＝______________．