如图p是等边三角形abc内的一点,∠APB比∠BPC比∠CPA=5比6比7答案解析
科目:czsx
来源:
题型:
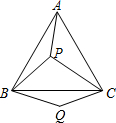
(2012•仪陇县模拟)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
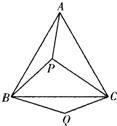
26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点P是等边三角形ABC内的一点,若将△PAB绕点A逆时针旋转到△P′AC,则∠PAP′的度数为
60°
60°
.
查看答案和解析>>
科目:czsx
来源:
题型:
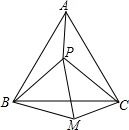
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.
(1)观察并猜想AP与CM之间的大小关系,并说明你的结论;
(2)若PA=PB=PC,则△PMC是
三角形;
(3)若PA:PB:PC=1:
:
,试判断△PMC的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
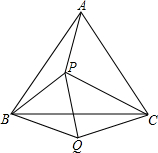
如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°,且BQ=BP,连
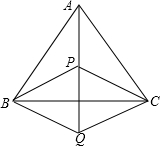
接CQ.
(1)试观察并猜想AP与CQ的大小关系;
(2)证明你在(1)中的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,P是等边三角形ABC内的一点,若将△PAC绕点A逆时针旋转到△P′AB,则∠PAP′的度数为( )
查看答案和解析>>
科目:czsx
来源:
题型:

21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.
查看答案和解析>>
科目:czsx
来源:
题型:
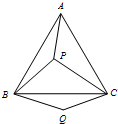
18、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
查看答案和解析>>
科目:czsx
来源:
题型:

(2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
题目1:如图①,在△ABC中,AC=BC,∠ACB=90°,O为△ABC内的一点,OC=1,OA=
,OB=
.求∠AOC的度数.
小明去请教小颖正在解答下列题目.
题目2:如图②,点O是等边三角形ABC内的一点,将△BCO绕C顺时针方向旋转60°得到△ADC,连接OD.
(1)试判断△COD的形状,并说明理由;
(2)当∠COB=150°时,试判断△AOD的形状,并写出OA、OB、OC三者之间的等量关系式.
小颖说:“等等,等我做完了,我们一起来看.”小明看完,小颖做完后高兴地说:“哈哈,太好了,我会了.”聪明的同学,你能先解答完题目2,再根据解答所得到的启迪来完成题目1吗?写出你的解答过程.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并说明理由.
(2)若PA=3,PB=4,PC=5,∠BQC=
150°
150°
.(请直接写出∠BQC的度数)
查看答案和解析>>
科目:czsx
来源:
题型:

(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是
(不取近似值).
查看答案和解析>>
科目:czsx
来源:2011年江苏省邳州市运河中学八年级(上)期中测试数学卷
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
(12分)如图,P是等边三角形ABC内的一点,连结PA、PB、PC,以BP为边作等边三角形BPM,连结CM.

(1)观察并猜想AP与CM之间的大小关系,并说明你的结论;
(2)若PA:PB:PC=1:

:

,试判断△PMC的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(12分)如图,P是等边三角形ABC内的一点,连结PA、PB、PC,以BP为边作等边三角形BPM,连结CM.
(1)观察并猜想AP与CM之间的大小关系,并说明你的结论;
(2)若PA:PB:PC=1: :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:2011年江苏省邳州市八年级(上)期中测试数学卷
题型:解答题
(12分)如图,P是等边三角形ABC内的一点,连结PA、PB、PC,以BP为边作等边三角形BPM,连结CM.
(1)观察并猜想AP与CM之间的大小关系,并说明你的结论;
(2)若PA:PB:PC=1: :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
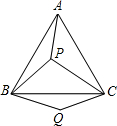 如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
查看答案和解析>>
科目:czsx
来源:宜宾
题型:填空题
(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P′外,则sin∠PCP′的值是______(不取近似值).
查看答案和解析>>
科目:czsx
来源:湖南省中考真题
题型:解答题
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ。
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由。
查看答案和解析>>
科目:czsx
来源:2012年湖北省荆州市洪湖市中考数学模拟试卷(二)(解析版)
题型:解答题
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.

查看答案和解析>>

 (2012•仪陇县模拟)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
(2012•仪陇县模拟)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论. 26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ. 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM. 接CQ.
接CQ. 21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.
21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角. 18、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
18、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ. (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了. 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ. (按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
 :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由.
 :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由. ![]() :
:![]() ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由. :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由. 如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.

