已知正方体ABCD-A'B'C'D'求证A'C⊥AB'D'答案解析
科目:gzsx
来源:
题型:
已知正方体ABCD-A′B′C′D′中,点F是侧面CDD′C′的中心,若
=
+x
+y
,则x-y等于( )
查看答案和解析>>
科目:gzsx
来源:
题型:
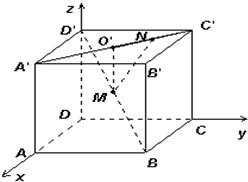
如图,已知正方体ABCD-A'B'C'D'的棱长为a,M为BD'的中点,点N在AC'上,且|A'N|=3|NC'|,试求MN的长.
查看答案和解析>>
科目:gzsx
来源:
题型:

如图所示,已知正方体ABCD-A′B′C′D′,求:
(1)BC′与CD′所成的角;
(2)AD与BC′所成的角.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A'B'C'D',下面有关说法中不正确的是( )
|
|
|
|
查看答案和解析>>
科目:gzsx
来源:
题型:
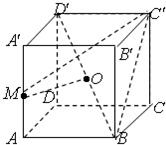
已知正方体ABCD-A′B′C′D′的棱长为1,点M是棱AA′的中点,点O是对角线BD′的中点.
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
(Ⅲ)求三棱锥M-OBC的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
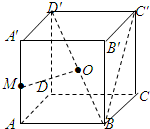
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
(Ⅱ)求三棱锥M-OBC的体积;
(Ⅲ)求二面角M-BC'-B'的正切值.
查看答案和解析>>
科目:gzsx
来源:
题型:
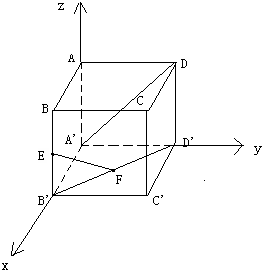
已知正方体ABCD-A′B′C′D′中,点E、F分别是棱BB′与面对角线B′D′的中点,求证:直线EF⊥直线A′D.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A'B'C'D',则该正方体的体积、四棱锥C'-ABCD的体积以及该正方体的外接球的体积之比为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
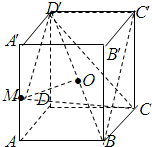
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
(Ⅰ)求证:OM⊥平面BDD′;
(Ⅱ)A′B′上是否存在点N使A′N∥面MCD′,并证明你的结论;
(Ⅲ)求三棱锥M-OBC的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
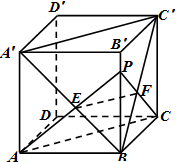
已知正方体ABCD-A′B′C′D′,P是线段BB'上的异于端点B、B′的点,设PA∩A′B=E,PC∩BC′=F.
(1)当P是BB′中点时,异面直线PC、AD所成角的正切值;
(2)求证:EF∥面ABCD.
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,已知正方体ABCD—A′B′C′D′.
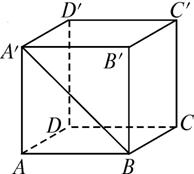
①哪些棱所在直线与直线BA′是异面直线?
②直线BA′和CC′的夹角是多少?
③哪些棱所在的直线与直线AA′垂直?
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,已知正方体ABCD—A′B′C′D′.

①哪些棱所在直线与直线BA′是异面直线?
②直线BA′和CC′的夹角是多少?
③哪些棱所在的直线与直线AA′垂直?
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,已知正方体ABCD—A′B′C′D′.
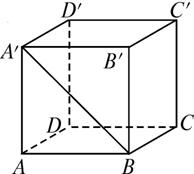
①哪些棱所在直线与直线BA′是异面直线?
②直线BA′和CC′的夹角是多少?
③哪些棱所在的直线与直线AA′垂直?
查看答案和解析>>
科目:gzsx
来源:2010-2011学年广东省广州市增城中学高二(上)周考数学试卷(8)(10.31)(解析版)
题型:解答题
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
(Ⅱ)求三棱锥M-OBC的体积;
(Ⅲ)求二面角M-BC'-B'的正切值.

查看答案和解析>>
科目:gzsx
来源:
题型:
如图,已知正方体
ABCD—
A′
B′
C′
D′,点
E是上底面
A′
B′
C′
D′的中心,求下列各式中
x、
y、
z的值.

(1) ;
;
(2) .
.
查看答案和解析>>
科目:gzsx
来源:2007-2008学年山东省实验中学高二(上)期末数学试卷(理科)(解析版)
题型:选择题
已知正方体ABCD-A′B′C′D′中,点F是侧面CDD′C′的中心,若

=

+x

+y

,则x-y等于( )
A.0
B.1
C.

D.-

查看答案和解析>>
科目:gzsx
来源:2012-2013学年安徽省黄山市屯溪一中高二(上)期中数学试卷(文科)(解析版)
题型:填空题
已知正方体ABCD-A'B'C'D',则该正方体的体积、四棱锥C'-ABCD的体积以及该正方体的外接球的体积之比为 .
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省济南市世纪英华实验学校高二(上)期末数学试卷(理科)(解析版)
题型:解答题
已知正方体ABCD-A′B′C′D′中,点E、F分别是棱BB′与面对角线B′D′的中点,求证:直线EF⊥直线A′D.

查看答案和解析>>

 已知正方体ABCD-A′B′C′D′的棱长为1,点M是棱AA′的中点,点O是对角线BD′的中点.
已知正方体ABCD-A′B′C′D′的棱长为1,点M是棱AA′的中点,点O是对角线BD′的中点. 已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点. 已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点. 已知正方体ABCD-A′B′C′D′,P是线段BB'上的异于端点B、B′的点,设PA∩A′B=E,PC∩BC′=F.
已知正方体ABCD-A′B′C′D′,P是线段BB'上的异于端点B、B′的点,设PA∩A′B=E,PC∩BC′=F.

![]() 中,E、F分别是AB、AA1的中点,则平面CEB1与平面D1FB1所成二面角的平面角的正弦值为
中,E、F分别是AB、AA1的中点,则平面CEB1与平面D1FB1所成二面角的平面角的正弦值为![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1

![]() =x
=x![]() +y
+y![]() +z
+z![]() ;
;![]() =x
=x![]() +y
+y![]() +z
+z![]() .
.

 =
= +x
+x +y
+y ,则x-y等于( )
,则x-y等于( )

