3个等边三角形 请分别把他们分成两个,三个, 四个全等的三角形答案解析
科目:czsx
来源:数学教研室
题型:044
等边三角形给人以“稳如泰山”的美感,它具有独特的对称性,下图是三个等边三角形,请分别把他们分成两个、三个、四个全等的三角形:

查看答案和解析>>
科目:czsx
来源:
题型:
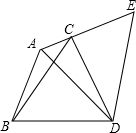
如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.
(1)求∠BAD的度数;
(2)求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,在△ABC中,若AB=5,AC=2,

BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。

【小题1】(1)求

BAD的度数;
【小题2】(2)求AE的长。
查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市154中九年级上学期期中考试数学卷
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,在△ABC中,若AB=5,AC=2, BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。

1.(1)求 BAD的度数;
BAD的度数;
2.(2)求AE的长。
查看答案和解析>>
科目:czsx
来源:2011-2012年北京市九年级上学期期中考试数学卷
题型:解答题
如图所示,在△ABC中,若AB=5,AC=2, BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。

1.(1)求 BAD的度数;
BAD的度数;
2.(2)求AE的长。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.
如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.
(1)求∠BAD的度数;
(2)求AE的长.
查看答案和解析>>
科目:czsx
来源:北京市期末题
题型:解答题
如图,在△ABC中,若AB=5,AC=2,∠BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
(1)求∠BAD的度数;
(2)求AE的长.
查看答案和解析>>
科目:czsx
来源:期末题
题型:操作题
请你画一个20°、40°、120°角的三角形,再把它分成两个等腰三角形,有几种分法,请你设计并将它画出来。
查看答案和解析>>
科目:czsx
来源:
题型:
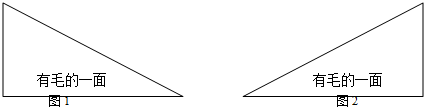
26、王华在某制衣厂工作,他应按设计师的要求在衣服上镶嵌一种直角三角形形状的皮草(如图1).但王华不小心裁反了,裁成如图2的形状.为了不浪费昂贵的材料,聪明的王华发现只要在裁反的材料(图2)上剪一刀,把图2分成两块,就可以再拼成图1的形状.请在图2中画出裁剪线(要求:尺规作图,保留作图痕迹,不写作法.)
查看答案和解析>>
科目:czsx
来源:
题型:

用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
(1)它最多需要多少个小正方体?
(2)它最少需要多少个小正方体?请分别画出这两种情况下从左面看该几何体得到的图形.
查看答案和解析>>
科目:czsx
来源:2007年江苏省无锡市北塘区中考数学一模试卷(解析版)
题型:解答题
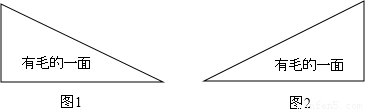
王华在某制衣厂工作,他应按设计师的要求在衣服上镶嵌一种直角三角形形状的皮草(如图1).但王华不小心裁反了,裁成如图2的形状.为了不浪费昂贵的材料,聪明的王华发现只要在裁反的材料(图2)上剪一刀,把图2分成两块,就可以再拼成图1的形状.请在图2中画出裁剪线(要求:尺规作图,保留作图痕迹,不写作法.)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
(1)它最多需要多少个小正方体?
(2)它最少需要多少个小正方体?请分别画出这两种情况下从左面看该几何体得到的图形.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
王华在某制衣厂工作,他应按设计师的要求在衣服上镶嵌一种直角三角形形状的皮草(如图1).但王华不小心裁反了,裁成如图2的形状.为了不浪费昂贵的材料,聪明的王华发现只要在裁反的材料(图2)上剪一刀,把图2分成两块,就可以再拼成图1的形状.请在图2中画出裁剪线(要求:尺规作图,保留作图痕迹,不写作法.)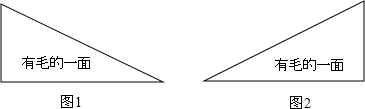
查看答案和解析>>
科目:czsx
来源:
题型:
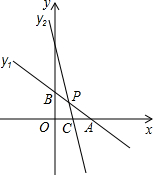
如图,在平面直角坐标系xOy中,一次函数
y1=-x+2与x轴、y轴分别相交于点A和点B,直线y
2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求A、B的坐标;
(2)求△ABO的面积;
(3)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在平面直角坐标系xOy中,一次函数
如图,在平面直角坐标系xOy中,一次函数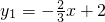 与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求A、B的坐标;
(2)求△ABO的面积;
(3)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
查看答案和解析>>
科目:czsx
来源:2009年江苏省南京市江宁区中考数学二模试卷(解析版)
题型:解答题
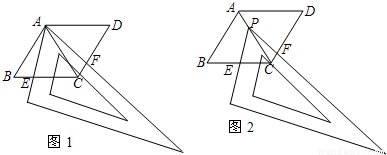
把两个边长都等于4的等边三角形拼成菱形ABCD(如下图).有一个含60°角的三角尺,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.
(1)将三角尺绕点A按逆时针方向旋转,当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时(如图1),通过观察或测量AE,AF的长度,你能得出什么结论?并证明你的结论;
(2)在旋转过程中四边形AECF的周长是否发生变化?如果没有变化,请说明理由;如果有变化,请求出周长的最小值;
(3)若将(1)中三角尺的60°角的顶点P在AC上移动且与点A、C都不重合,三角尺的两边分别与菱形的两边BC、CD相交于点E、F时(如图3),那么PE、PF之间又有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:

在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形
(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于
?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
13、如图是等边三角形,你能把它分成两个全等的三角形吗?你能把它分成3个、4个全等的三角形吗?(分别画在三个三角形内)

查看答案和解析>>
科目:czsx
来源:
题型:
已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DG∥BC交AC于点G.DE⊥BC于点E,过点G作GF⊥BC于点F,把三角形纸片ABC分别沿DG,DE,GF按图1所示方式折叠,点A,B,C分别落在点A′,B′,C′处.若点A′,B′,C′在矩形DEFG内或其边上,且互不重合,此时我们称△A′B′C′(即图中阴影部分)为“重叠三角形”.
(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在.试用含m的代数式表示重叠
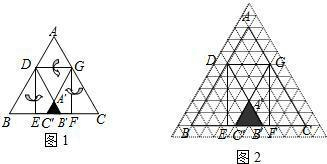
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
查看答案和解析>>

 如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.
如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置. BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
 BAD的度数;
BAD的度数; BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
 BAD的度数;
BAD的度数; BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
![]() BAD的度数;
BAD的度数; BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
BAC=120°,以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。
 BAD的度数;
BAD的度数; 如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.
如图,在△ABC中,若AB=5,AC=2,∠BAC=120°.以BC为边作等边三角形BCD,把△ABD绕D点按顺时针方向旋转60°到△ECD的位置.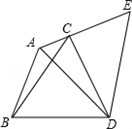

 用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
 用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
 如图,在平面直角坐标系xOy中,一次函数y1=-
如图,在平面直角坐标系xOy中,一次函数y1=- 如图,在平面直角坐标系xOy中,一次函数
如图,在平面直角坐标系xOy中,一次函数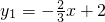 与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
 在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形
在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)