若有理数m小于n小于0,试判断(m+n)与(m-n)的及的符号答案解析
科目:czsx
来源:
题型:

25、如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
(1)作点P,使它与点O关于点E成中心对称,连接CP、DP;
(2)若四边形ABCD是矩形,试判断(1)中所得四边形CODP的形状并说明理由;
(3)若(1)中所得四边形CODP是正方形,请用图中的字母和符号表示四边形ABCD应满足的条件:
OC=OD,AC⊥BD
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
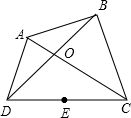 如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
(1)作点P,使它与点O关于点E成中心对称,连接CP、DP;
(2)若四边形ABCD是矩形,试判断(1)中所得四边形CODP的形状并说明理由;
(3)若(1)中所得四边形CODP是正方形,请用图中的字母和符号表示四边形ABCD应满足的条件:______.
查看答案和解析>>
科目:czsx
来源:
题型:
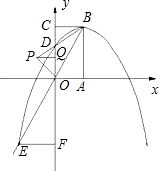
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax
2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:2013年江苏省中考数学预测试卷(一)(解析版)
题型:解答题
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax
2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.

查看答案和解析>>
科目:czsx
来源:2012年江苏省南通市中考数学模拟试卷(十)(解析版)
题型:解答题
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax
2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.

查看答案和解析>>
科目:czsx
来源:2009年湖北省宜昌市枝江市英杰学校中考数学模拟试卷(刘永洪)(解析版)
题型:解答题
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax
2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.

查看答案和解析>>
科目:czsx
来源:2011年山东省德州市陵县郑寨中学中考数学模拟试卷(解析版)
题型:解答题
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax
2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
把直线y=-2x+2沿x轴翻折恰好与抛物线y=ax2+bx+2交于点C(1,0)和点A(8,m).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,设点P是x轴上的任意一点(点P与点C不重合),若S△ABC=S△ACP,求满足条件的P点的坐标;
(3)设点P是x轴上的任意一点,试判断:PA+PB与AC+BC的大小关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
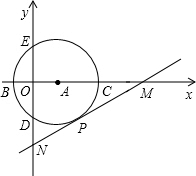
如图,在直角坐标系中,以点A(
,0)为圆心,以
2为半径的圆与x轴交于B、C两点,与y轴交于D、E两点.
(1)求D点坐标.
(2)若B、C、D三点在抛物线y=ax
2+bx+c上,求这个抛物线的解析式.
(3)若⊙A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30°,试判断直线MN是否经过所求抛物线的顶点?说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x
1,x
2,x
3,…,x
n的n个正方形依次放入△ABC中,请回答下列问题:
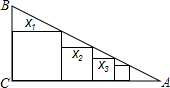
(1)按要求填表:
(2)第n个正方形的边长x
n=
;
(3)若m,n,p,q是正整数,且x
m•x
n=x
p•x
q,试判断m,n,p,q的关系.
查看答案和解析>>
科目:czsx
来源:
题型:
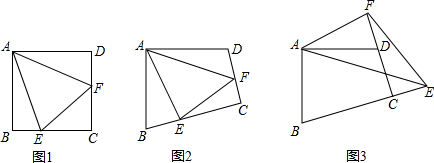
(2012•怀柔区一模)探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:
EF=BE+DF
EF=BE+DF
;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=
∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读下列材料:
试判断a
2-3a+7与-3a+2的大小.
分析:要判断两个数的大小,我们往往用作差法,即若a-b>0,则a>b;若a-b<0,则a<b;若a-b=0,则a=b.
解:∵(a
2-3a+7)-(-3a+2)=a
2-3a+7+3a-2
=a
2+5,
又∵a
2>0,∴a
2+5>0.
∴a
2-3a+7>-3a+2.
阅读后,应用这种方法比较
与
的大小.
查看答案和解析>>
科目:czsx
来源:
题型:

a、b两数在数轴上的位置如图所示,若设M=a+b,N=-a+b,H=a-b,G=-a-b.试判断M、N、G、H的大小.
查看答案和解析>>
科目:czsx
来源:
题型:
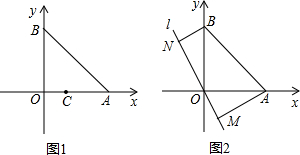
平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个?
(2)过A、B向直线l:y=-2x作垂线,垂足分别为M,N(如图2),试判断线段AM、BN、MN之间的数量关系,并说明理由.
(3)过A、B向动直线l:y=kx(k>0)作垂线,垂足分别为M,N,请直接写出线段AM、BN、MN之间的数量关系.
查看答案和解析>>
科目:czsx
来源:
题型:
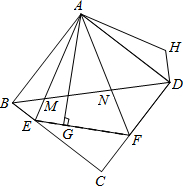
如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
探究一:猜想:四边形ABCD是何种特殊的四边形?请证明自己的猜想.
探究二:连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段 MN
2、ND
2、DH
2之间的数量关系,并说明理由.
探究三:若EG=4,GF=6,BM=3
,你能求出AG、MN的长吗?
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•德庆县二模)如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3
,求AG、MN的长.
查看答案和解析>>
科目:czsx
来源:
题型:
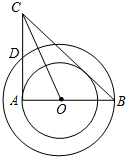
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留π)
查看答案和解析>>
科目:czsx
来源:
题型:

25、如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.
查看答案和解析>>
科目:czsx
来源:
题型:
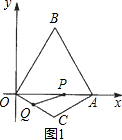
已知:如图(1),在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
(2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
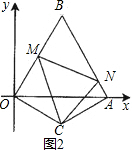
(3)如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
查看答案和解析>>

 25、如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
25、如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点. 如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点. 如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.



 如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q. 如图,在直角坐标系中,以点A(
如图,在直角坐标系中,以点A(

 平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
平面直角坐标系xOy中,已知定点A(1,0)和B(0,1). 如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C. (2013•德庆县二模)如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(2013•德庆县二模)如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C. 21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 25、如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
25、如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
