
科目:gzsx 来源: 题型:
(08年宁夏、海南卷文)(本小题满分12分)设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)证明:曲线![]() 上任一点处的
上任一点处的
切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
科目:gzsx 来源: 题型:
(08年宁夏、海南卷理)(本小题满分12分)
设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为y=3.
处的切线方程为y=3.
(Ⅰ)求![]() 的解析式:
的解析式:
(Ⅱ)证明:函数![]() 的图像是一个中心对称图形,并求其对称中心;
的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线![]() 上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
科目:gzsx 来源:2014届山东省济宁市高二3月月考数学文科试卷(解析版) 题型:解答题
(本小题满分12分)
设函数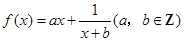 ,曲线
,曲线 在点
在点 处的切线方程
处的切线方程 .
.
(1)求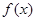 的解析式,并判断函数
的解析式,并判断函数 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
(2)证明:曲线 上任一点的切线与直线
上任一点的切线与直线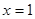 和直线
和直线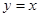 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
(3) 将函数 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线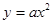 (
( 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)
科目:gzsx 来源:2010年山西省平遥中学高二下学期期中考试数学(文) 题型:解答题
(本小题满分12分 )
)
已知直线 为曲线
为曲线 在点
在点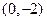 处的切线,
处的切线, 为该曲线的另一条切线,
为该曲线的另一条切线,
且 .
.
(Ⅰ )求直线
)求直线 的方程;
的方程;
(Ⅱ)求由直线 ,
,  和
和 轴所围成的三角形的面积
轴所围成的三角形的面积
科目:gzsx 来源:2011-2012学年山东省高三教学质量检测(四)文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
设函数 ,曲线
,曲线 在点(2,
在点(2, (2))处的切线方程为
(2))处的切线方程为
(Ⅰ)求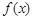 的解析式;
的解析式;
(Ⅱ)若 对一切
对一切 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)证明:曲线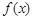 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为一值,并求此定值。
所围成的三角形面积为一值,并求此定值。
科目:gzsx 来源:2010年山西省高二下学期期中考试数学(文) 题型:解答题
(本小题满分12分)
已知直线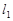 为曲线
为曲线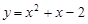 在点
在点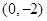 处的切线,
处的切线,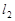 为该曲线的另一条切线,
为该曲线的另一条切线,
且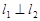 .
.
(Ⅰ)求直线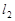 的方程;
的方程;
(Ⅱ)求由直线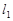 ,
, 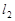 和
和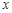 轴所围成的三角形的面积
轴所围成的三角形的面积
科目:gzsx 来源: 题型:
(本小题满分13分)
已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,若函数
,若函数![]() 与
与![]() 轴有两个交点,求实数
轴有两个交点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)证明:曲线![]() 上任意一点的切线与直线
上任意一点的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求出此定值.
所围成的三角形面积为定值,并求出此定值.
科目:gzsx 来源:2012-2013学年吉林长春实验中学高三上学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
设函数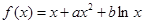 ,曲线
,曲线 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.
(1)求 的值;
的值;
(2)证明:
科目:gzsx 来源:2010-2011学年四川省高三第七次月考理科数学卷 题型:解答题
(本小题满分12分)
设函数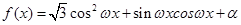 (其中
(其中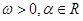 ),且
),且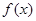 的图象在
的图象在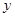 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为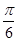 。
。
(Ⅰ)求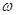 的值。
的值。
(Ⅱ)如果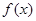 在区间
在区间 上的最小值为
上的最小值为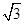 ,求
,求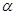 的值。
的值。
科目:gzsx 来源: 题型:
(本小题满分12分)设函数![]() 若它是R上的单调函数,且1是它的零点。
若它是R上的单调函数,且1是它的零点。
(1)求实数a的值;
|
科目:gzsx 来源:2010年大连市高二六月月考理科数学卷 题型:解答题
(本小题满分12分)
设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数f(x)的单调性。
科目:gzsx 来源:2012-2013学年河南灵宝第三高级中学高三上学期第三次质量检测文数学试卷(解析版) 题型:解答题
(本小题满分12分)
设函数
(Ⅰ)若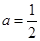 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若当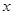 ≥0时
≥0时 ≥0,求
≥0,求 的取值范围.
的取值范围.
科目:gzsx 来源:2015届浙江宁波金兰合作组织高一上学期期中联考数学试卷(解析版) 题型:解答题
(本小题满分12分)
设 ,且
,且 ,定义在区间
,定义在区间 内的函数
内的函数 是奇函数.
是奇函数.
(1)求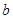 的取值范围;
的取值范围;
(2)讨论函数 的单调性并证明.
的单调性并证明.
科目:gzsx 来源:2011年福建省高一上学期期中考试数学 题型:解答题
(本小题满分12分)
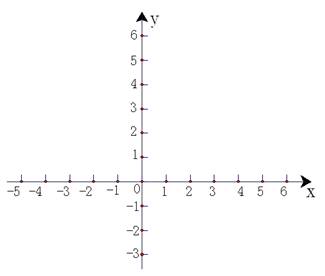
设函数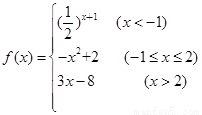 .
.
(Ⅰ)请在下列直角坐标系中画出函数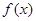 的图象;
的图象;
(Ⅱ)根据(Ⅰ)的图象,试分别写出关于 的方程
的方程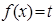 有2,3,4个实数解时,相应的实数
有2,3,4个实数解时,相应的实数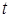 的取值范围;
的取值范围;
(Ⅲ)记函数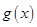 的定义域为
的定义域为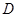 ,若存在
,若存在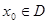 ,使
,使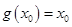 成立,则称点
成立,则称点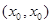 为函数
为函数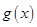 图象上的不动点.试问,函数
图象上的不动点.试问,函数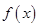 图象上是否存在不动点,若存在,求出不动点的坐标,若不存在,请说明理由.
图象上是否存在不动点,若存在,求出不动点的坐标,若不存在,请说明理由.
科目:gzsx 来源:2013届云南省高二下期中理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
设函数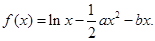
(Ⅰ)当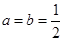 时,求
时,求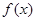 的最大值;
的最大值;
(Ⅱ)令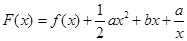 ,(
,(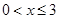 ),其图象上任意一点
),其图象上任意一点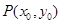 处切线的斜率
处切线的斜率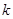 ≤
≤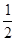 恒成立,求实数
恒成立,求实数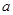 的取值范围;
的取值范围;
科目:gzsx 来源:2010年河南省实验中学高一下学期期中考试数学 题型:解答题
(本小题满分12分)设函数 .
.
(1)写出 的最大值M,最小值m,最小正周期T;
的最大值M,最小值m,最小正周期T;
(2)试求最小正整数k,使得当自变量x在任意两个整数间(包括整数本身)变化时,函数 至少有一个值是M和一个值是m .
至少有一个值是M和一个值是m .
科目:gzsx 来源:2010-2011年吉林省汪清六中高二第二学期3月月考数学文卷 题型:解答题
(本小题满分12分)
设函数 是定义域在
是定义域在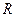 ,并且满足
,并且满足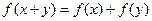 ,
, ,且当
,且当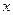 >0时,
>0时, <0。
<0。
(1)求 的值,
的值,
(2)判断函数的奇偶性,
(3)如果 ,求
,求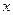 的取值范围。
的取值范围。
科目:gzsx 来源:2011-2012学年山东省高三下学期5月高考冲刺文科数学(解析版) 题型:解答题
(本小题满分12分)设函数 .
.
(I)求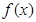 的单调区间;
的单调区间;
(II)当0<a<2时,求函数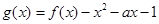 在区间
在区间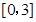 上的最小值.
上的最小值.
科目:gzsx 来源:2011-2012学年河北省高三12月月考试题理科数学 题型:解答题
(本小题满分12分)
设函数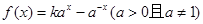 是定义域为R上的奇函数;
是定义域为R上的奇函数;
(Ⅰ)若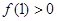 ,试求不等式
,试求不等式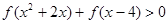 的解集;
的解集;
(Ⅱ)若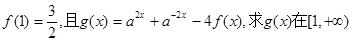 上的最小值。
上的最小值。