
科目:czsx 来源: 题型:
 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):
科目:czsx 来源: 题型:
 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):
科目:czsx 来源: 题型:
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题: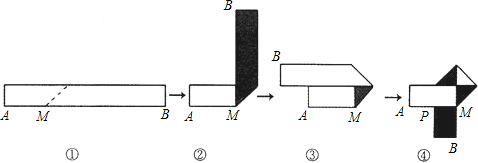
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 ,宽为
,宽为 ,分别回答下列问题:
,分别回答下列问题: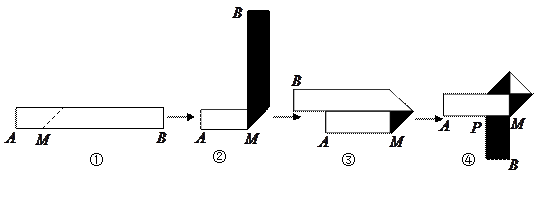
 ),试求
),试求 的取值范围.
的取值范围. 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(用
的距离(用 表示)
表示) 科目:czsx 来源: 题型:
生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为26厘米,回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BM=_____厘米;在图④中,BM=_____厘米.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是对称图形,假设长方形纸条的宽为![]() 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含![]() 的代数式表示).
的代数式表示).
科目:czsx 来源:2014届江苏省无锡市七年级下学期期中考试数学卷(解析版) 题型:解答题
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长为26厘米,回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BM=_____厘米;在图④中,BM=_____厘米.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是对称图形,假设长方形纸条的宽为 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含 的代数式表示).
的代数式表示).
科目:czsx 来源:2011-2012学年江苏省无锡市育才中学七年级下学期期中考试数学卷(带解析) 题型:解答题
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):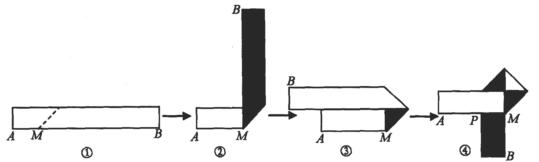
如果由信纸折成的长方形纸条(图①)长为26厘米,回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BM=_____厘米;在图④中,BM=_____厘米.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是对称图形,假设长方形纸条的宽为 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含 的代数式表示).
的代数式表示).
科目:czsx 来源: 题型:
 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):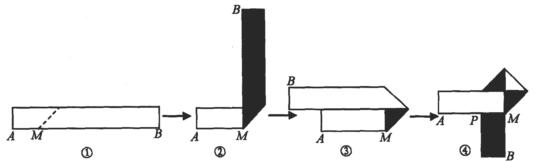
 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含 的代数式表示).
的代数式表示). 科目:czsx 来源:2011年广东省徐闻县第一中学初一第一学期期末考试数学卷 题型:解答题
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 ,宽为
,宽为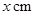 ,分别回答下列问题:
,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点 ),试求
),试求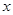 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(用
的距离(用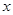 表示)
表示)
科目:czsx 来源:2007年山东省烟台市中考数学试卷(解析版) 题型:解答题
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
科目:czsx 来源: 题型:解答题
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
科目:czsx 来源:2007年烟台市初中毕业升学统一考试、数学试题 题型:059
生活中,有人喜欢把传送的便条折成形状![]() ,折叠过程是这样的(阴影部分表示纸条的反面):
,折叠过程是这样的(阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长为26 cm,宽为xcm,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).
科目:czsx 来源:浙江省期末题 题型:解答题
 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面): 
 cm,分别回答下列问题:
cm,分别回答下列问题: 的取值范围;
的取值范围; 表示)。
表示)。 科目:czsx 来源: 题型:
![]() 生活中,有人喜欢把传送的便条折成形状 ,折叠过程是这样的(阴影部分表示纸条的反面):
生活中,有人喜欢把传送的便条折成形状 ,折叠过程是这样的(阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).
科目:czsx 来源:2007年全国中考数学试题汇编《图形的对称》(04)(解析版) 题型:解答题
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题: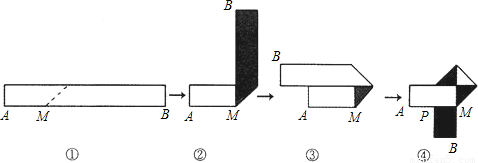
科目:czsx 来源: 题型:解答题
 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):
科目:czsx 来源:2009年河南省中招数学模拟试卷(6)(解析版) 题型:选择题

科目:czsx 来源:2010-2011学年浙江省杭州市留下中学九年级(上)期末数学试卷(解析版) 题型:解答题
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
科目:czsx 来源:第25章《图形的变换》中考题集(34):25.3 轴对称变换(解析版) 题型:解答题
 ,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题: