
科目:gzsx 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源:2011-2012学年湖南省怀化高中高二(下)期中数学试卷(文理合卷)(解析版) 题型:填空题
科目:gzsx 来源:2011-2012学年湖南省怀化高中高二(下)期中数学试卷(文理合卷)(解析版) 题型:填空题
科目:gzsx 来源: 题型:
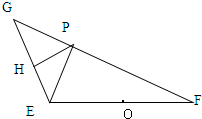 如图,已知|
如图,已知|| EF |
| FG |
| EH |
| EG |
| EO |
| EF |
| HP |
| EG |
| OC |
| c2 |
| a |
| OF |
| OM |
| OQ |
| QM |
科目:gzsx 来源: 题型:
| 2 |
| x2 |
| a2 |
科目:gzsx 来源: 题型:
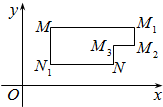
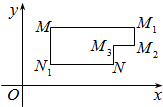 (2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.
(2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.科目:gzsx 来源: 题型:
| π | 3 |
科目:gzsx 来源:2012-2013学年湖北省高一理科实验班预录模拟数学试卷(解析版) 题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.

(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
科目:gzsx 来源:2014届吉林省高二4月月考理科数学试卷(解析版) 题型:解答题
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.


(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
科目:gzsx 来源:2004年上海市春季高考数学试卷(解析版) 题型:解答题
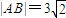 .
.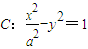 (a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;科目:gzsx 来源: 题型:
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的距离h关于t的函数关系式.
科目:gzsx 来源:学习高手必修二数学苏教版 苏教版 题型:022
在空间直角坐标系中,写出点P(x,y,z)的对称点的坐标.
(1)关于x轴的对称点是P1________;
(2)关于y轴的对称点是P2________;
(3)关于z轴的对称点是P3________;
(4)关于原点的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点是P6________;
(7)关于zOx坐标平面的对称点是P7________.
科目:gzsx 来源: 题型:
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P 与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的 距离h关于t的函数关系式.
科目:gzsx 来源:2012年云南省昆明市高三复习教学质量检测数学试卷(文科)(解析版) 题型:解答题
 ,直线l经过点P,倾斜角为α.
,直线l经过点P,倾斜角为α.科目:gzsx 来源:湖南 题型:解答题
科目:gzsx 来源:数学教研室 题型:044
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称![]() 的最小值为P与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的距离h关于t的函数关系式.
的最小值为P与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的距离h关于t的函数关系式.