
科目:czsx 来源: 题型:
已知:如图14,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)写出直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
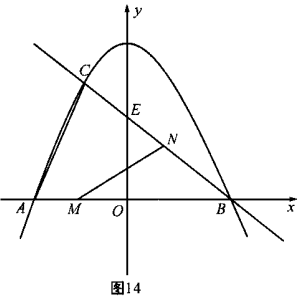 (3)若点
(3)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从![]() 向
向![]() 运动(不与
运动(不与![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从![]() 向
向![]() 运动.设运动时间为
运动.设运动时间为![]() 秒,请写出
秒,请写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 运动多少时间时,
运动多少时间时,![]() 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
科目:czsx 来源: 题型:
已知,如图(a),抛物线y=ax2+bx+c经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N.∠ONE=30°,|x1-x2|=8.
(1)求抛物线的解析式及顶点D的坐标;
(2)连结AD、BD,在![]() (1)中的抛物线上是否存在一点P,使得⊿ABP与⊿ADB相似?若存在,求出
(1)中的抛物线上是否存在一点P,使得⊿ABP与⊿ADB相似?若存在,求出![]() 点的坐标;若不存在,说明理由;
点的坐标;若不存在,说明理由;
(3)如图(b),点Q为![]() 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:
AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由.

科目:czsx 来源:2012届广西桂平市中考模拟训练题(一)数学试卷(带解析) 题型:解答题
已知,如图所示抛物线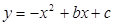 与x的两个交点分别为A(1,0),B(3,0)。
与x的两个交点分别为A(1,0),B(3,0)。
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB = 1这样的点P有几个?并求出所有点P 的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小.若存在,求出点M的坐标;若不存在,请说明理由.
科目:czsx 来源:2011-2012学年广西桂平市中考模拟训练题(一)数学试卷(解析版) 题型:解答题
已知,如图所示抛物线 与x的两个交点分别为A(1,0),B(3,0)。
与x的两个交点分别为A(1,0),B(3,0)。

(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB = 1这样的点P有几个?并求出所有点P 的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小.若存在,求出点M的坐标;若不存在,请说明理由.
科目:czsx 来源:2012年初中毕业升学考试(湖北鄂州卷)数学(解析版) 题型:解答题
已知:如图一,抛物线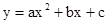 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
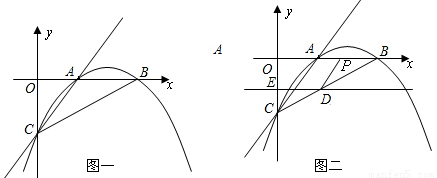
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
科目:czsx 来源:2011年北京市通州区中考二模数学试卷 题型:解答题
已知:如图14,⊙A与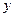 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为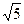 ,过点C作⊙A的切线交
,过点C作⊙A的切线交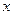 轴于点B(-4,0)
轴于点B(-4,0) .
.
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.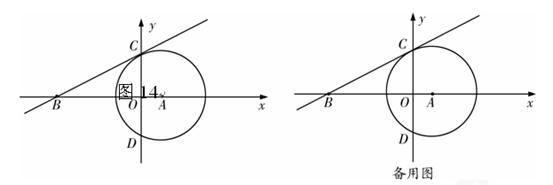
科目:czsx 来源: 题型:
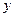 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为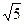 ,过点C作⊙A的切线交
,过点C作⊙A的切线交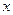 轴于点B(-4,0).
轴于点B(-4,0).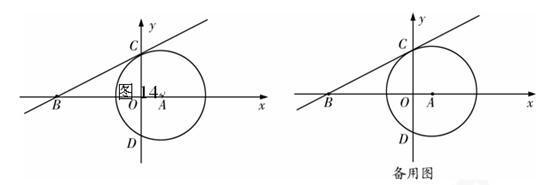
科目:czsx 来源:2012年初中毕业升学考试(湖北鄂州卷)数学(带解析) 题型:解答题
已知:如图一,抛物线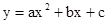 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设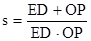 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
科目:czsx 来源: 题型:
| 5 | 2 |
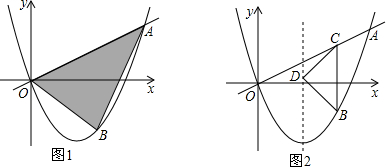
科目:czsx 来源: 题型:解答题
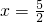 .点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
.点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
科目:czsx 来源:2012年四川省成都市铁路中学中考数学一模试卷(解析版) 题型:解答题
 .点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
.点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
科目:czsx 来源:2010-2011学年重庆市南开中学九年级(上)期末数学试卷(解析版) 题型:解答题
 .点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
.点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
科目:czsx 来源: 题型:
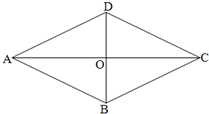 22、已知:如图,菱形ABCD的对角线交于点O,且AO、BO的长分别是方程x2-(2m-1)x+4(m-1)=0的两根,菱形ABCD的周长为20,求m的值.
22、已知:如图,菱形ABCD的对角线交于点O,且AO、BO的长分别是方程x2-(2m-1)x+4(m-1)=0的两根,菱形ABCD的周长为20,求m的值.科目:czsx 来源:2012届江苏省苏州市相城实验中学九年级10月月考数学卷 题型:解答题
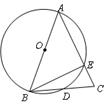
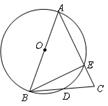
(本题满分10分)已知:如图,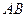 为
为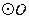 的直径,
的直径,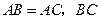 交
交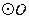 于点
于点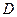 ,
,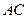 交
交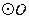 于点
于点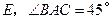 .
.
(1)求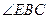 的度数;
的度数;
(2)求证: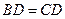 .
.
科目:czsx 来源:2011-2012学年江苏省苏州市九年级10月月考数学卷 题型:解答题
(本题满分10分)已知:如图,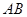 为
为 的直径,
的直径,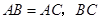 交
交 于点
于点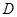 ,
,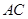 交
交 于点
于点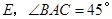 .
.
(1)求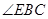 的度数;
的度数;
(2)求证: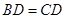 .
.