精英家教网 >
试题搜索列表 >如图在矩形ABCD 中点E是AD上的一点且AE比ED=1比2,BE与AC相交于点G
如图在矩形ABCD 中点E是AD上的一点且AE比ED=1比2,BE与AC相交于点G答案解析
科目:czsx
来源:
题型:
.(本小题10分)
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。

查看答案和解析>>
科目:czsx
来源:
题型:
.(本小题10分)
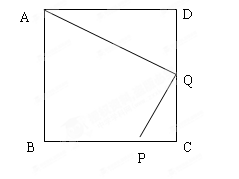
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
查看答案和解析>>
科目:czsx
来源:2012届浙江省九年级第二次月考数学卷
题型:解答题
.(本小题10分)
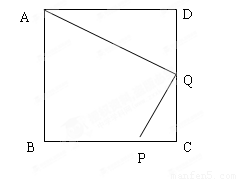
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
查看答案和解析>>
科目:czsx
来源:
题型:
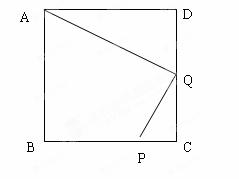
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
查看答案和解析>>
科目:czsx
来源:
题型:
已知:在平面直角坐标系中,抛物线y=ax
2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N
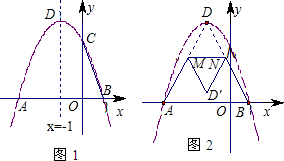
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:
平面上的点M关于直线l有唯一的轴对称点M′,这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系,我们把这种对应关系叫做点M关于直线l的轴对称变换,记为M
M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M
M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l)
M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)
M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
(1)在备用图中,请画出M′(l)和M″(l,m)(保留画图痕迹).
(2)当θ=
90
90
°时,M与M″(l,m)关于点O成中心对称.
(3)试探究∠MOM′′与θ之间的数量关系,并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
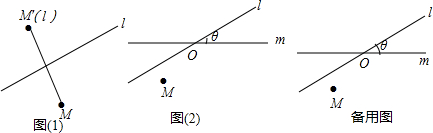
平面上的点M关于直线l有唯一的轴对称点M′,这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系,我们把这种对应关系叫做点M关于直线l的轴对称变换,记为
MM′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
MM′(l),得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
M′(l)Mn(l,m),这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
M′(l)Mn(l,m),M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
(1)在图(2)中,求作M′(l)和M′′(l,m).(要求保留作图痕迹)
(2)当θ=
°时,M与M′′(l,m)关于点O成中心对称.
(A)30(B)45(C)60(D)90
(3)(在以下两题中任选一题作答)
①试探讨∠MOM′′(l,m)与θ之间的数量关系,并证明你的结论.
②试探讨OM与OM′′(l,m)间的数量关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:

如图在△ABC中,D为BC上的一点,E为AD上的一点,BE的延长线交AC于点F,已知
=,
=(a,b为不小于2的整数),则
的值是
.
查看答案和解析>>
科目:czsx
来源:
题型:
(8分)如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状。

查看答案和解析>>
科目:czsx
来源:
题型:
如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状

查看答案和解析>>
科目:czsx
来源:2011年河南省虞城县贾寨镇初级中学九年级第一学期期中考试数学卷
题型:解答题
(8分)如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状。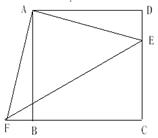
查看答案和解析>>
科目:czsx
来源:2011年河南省九年级第一学期期中考试数学卷
题型:解答题
(8分)如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状。
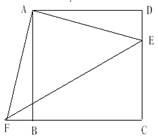
查看答案和解析>>
科目:czsx
来源:
题型:
(8分)如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状。
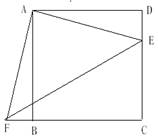
查看答案和解析>>
科目:czsx
来源:2011年河南虞城县贾寨镇初级中学九年级第一学期期中数学试卷
题型:解答题
如右图,正方形ABCD,E是CD上的一点,△ADE旋转后能与△ABF重合,请指出旋转中心和旋转角,并判断△AEF的形状

查看答案和解析>>
科目:czsx
来源:2011年浙江省嘉兴市南湖区余新中学中考数学模拟试卷(解析版)
题型:解答题
已知:在平面直角坐标系中,抛物线y=ax
2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.

查看答案和解析>>
科目:czsx
来源:2008年江苏省南京市建邺区中考数学一模试卷(解析版)
题型:解答题
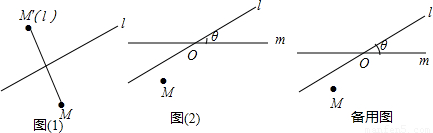
平面上的点M关于直线l有唯一的轴对称点M′,这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系,我们把这种对应关系叫做点M关于直线l的轴对称变换,记为
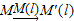
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
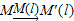
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
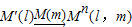
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
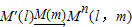
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
(1)在图(2)中,求作M′(l)和M′′(l,m).(要求保留作图痕迹)
(2)当θ=______°时,M与M′′(l,m)关于点O成中心对称.
(A)30(B)45(C)60(D)90
(3)(在以下两题中任选一题作答)
①试探讨∠MOM′′(l,m)与θ之间的数量关系,并证明你的结论.
②试探讨OM与OM′′(l,m)间的数量关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:在平面直角坐标系中,抛物线y=ax2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
查看答案和解析>>
科目:czsx
来源:2009年江苏省南京市中考数学模拟卷(解析版)
题型:解答题
(2008•建邺区一模)平面上的点M关于直线l有唯一的轴对称点M′,这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系,我们把这种对应关系叫做点M关于直线l的轴对称变换,记为
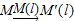
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
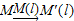
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
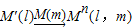
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为

,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
(1)在图(2)中,求作M′(l)和M′′(l,m).(要求保留作图痕迹)
(2)当θ=______°时,M与M′′(l,m)关于点O成中心对称.
(A)30(B)45(C)60(D)90
(3)(在以下两题中任选一题作答)
①试探讨∠MOM′′(l,m)与θ之间的数量关系,并证明你的结论.
②试探讨OM与OM′′(l,m)间的数量关系,并证明你的结论.

查看答案和解析>>


 ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值. 

 如图在△ABC中,D为BC上的一点,E为AD上的一点,BE的延长线交AC于点F,已知
如图在△ABC中,D为BC上的一点,E为AD上的一点,BE的延长线交AC于点F,已知



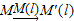 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换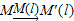 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换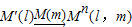 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为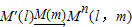 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
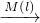 M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M
M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M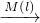 M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l)
M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l)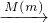 M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)
M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)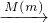 M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
 ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.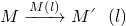 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换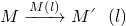 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换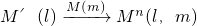 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为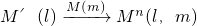 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: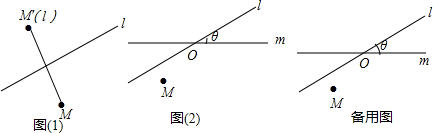
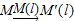 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换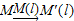 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换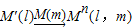 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: