练习册

  • 练习册
  • 试题
    (四)综合例题赏析 例4设点P在有向线段AB的延长线上.P分AB所在的比为λ.则 ( ) A.λ＜-1 B.-1＜λ＜0 C.0＜λ＜1 D.λ＞1 解 由已知有λ＝因为与的方向相反.且||＞||. 所以λ＝?||＜-1. 应选A. 例5 和直线3x-4y+5=0关于x轴对称的直线方程是( ) A.3x+4y-5=0 B.3x+4y+5=0 C.-3x+4y-5=0 D.-3x+4y+5=0 解: 若曲线c的方程f(x,y)=0.曲线c和c′关于x轴对称.则曲线c′的方程是f=0. ∴3x-4(-y)+5=0即3x+4y+5=0为所求. 应选B. 例6 如图.设图中直线l1.l2.l3的斜率分 别为k1.k2.k3.则( ) A.k1＜k2＜k3 B.k3＜k1＜k2 C.k3＜k2＜k1 D.k1＜k1＜k2 解 显然k1＜0.0＜k3＜k2 于是应选D. 例7 如果直线y=ax+2与直线y=3x-b关于直线y=x对称.那么( ) A.a=,b=6 B.a=,b=-6 C.a=3,b=-2 D.a=3,b=6 解 C1的方程是f(x,y)=0,C2和C1关于直线y=x对称.则C2的方程是f(y,x)=0. 于是直线y=ax+2关于直线y=x对称的直线的方程是x=ay+2,即y=. 由题设y=和y=3x-b是同一条直线. 所以.解得 从而应选A. 例8 通过点(0.2)且倾斜角为15°的直线方程是( ) A.y=(-2)x+2 B.y=(-1)x+2 C.y=(2-)x+2 D.y=(-1) x+2 解: ∵直线通过点(0.2). ∴直线在y轴上的截距b=2. ∵直线的倾角为15°. ∴直线的斜率k=tg15°=. 把k=2-.b=2代入直线的斜截式方程y=kx+b.得y=(2-)x+2 . 应选C. 例9 直线3x-2y=6在y轴上的截距是( ) A. B.-2 C. -3 D.3 解: ∵3x-2y=6y=-+=1. 又直线的截距为=1. ∴b=-3.即在y轴上的截距为-3. 应选C. 例10 如果直线ax+2y+2=0与直线3x-y-2=0平行.那么 系数a=( ) A.-3 B.-6 C.- D. 解:l1:A1x+B1y+C1=0.l2:A2x+B2y+C2=0.且A2≠0.B2≠0.C2≠ 0.则有 l1∥l2 ∴由题设有=a=- 6. 应选B. 例11 两条直线A1x+B1y+C1=0,A2x+B2y+C2=0垂直的充要条件是 ( ) A.A1A2+B1B2＝0 B.A1A2-B1B2＝0 C.＝-1 D. 解 若B1B2＝0.不妨设B1＝0.则直线l1∶A1x+C1=0.l1是垂直与x轴的直 线.由于l1⊥l2.所以l2是垂直y轴的直线.从而l2∶B2y+C2=0.即A2=0 故 A1A2+B1B2＝0 若B1B2≠0.则l1和l2的方程可化为y=-,y=-,得k1＝-.k2＝-, 由l1⊥l2k1·k2=-1·＝-1A1A2+B1B2＝0. 综上有若l1⊥l2.则A1A2+B1B2＝0 反之.若A1A2+B1B2＝0 1°A1A2≠0B1B2≠0A1A2＝-B1B2＝-· ＝-1()·()＝-1. 即k1·k2＝-1 所以l1⊥l2. 2°若A1·A2＝0.不妨设A1＝0.且A2≠0.则B1≠0且B1·B2＝0B2＝0 . 所以l1∶B1y+C1=0,是垂直y轴的直线, l2∶A2x+C2=0,是垂直x轴的直线, 于是l1⊥l2 又若A1＝0且A2＝0则l1∶B1y+C1=0,l2∶B2y+C2=0,则l1∥l2.此与 l1⊥l2矛盾. 综上有 若A1A2+B1B2＝0.则l1⊥l2 综合知.l1⊥l2A1A2＝B1B2＝0 故应选A. 例12 如果直线ax+2y+1=0与直线x+y-2=0互相垂直.那么a 的值等于( ) A.1 B.- C. - D.-2 解:两直线l1:A1x+B1y+C1=0.l2:A2x+B2y+C2=0.互相垂直的充要条件是 : A1A2+B1B2=0 ∴由题设得a·1+2·1=0.从而a=-2. 应选D. 例13 点P(2.5)关于直线x+y=0的对称点的坐标是( ) A. C. 解:设P关于直线y=-x对称.则PQ中点R(.)在y=-x上.且KPQ·(-1)=-1. ∴.解得 ∴对称点Q的坐标是. 应选C. 例14 原点关于直线8x+6y=25的对称点坐标是( ) A.(2.) B.(.) C. 解:设(m.n)为所求.则 解得m=4.n=3 ∴应选D. 例15 在直角坐标中.△ABC的三个顶点是:A.若直线x=a.将△ABC分割成面积相等的两部分.则实数a的值是( ) A. B.1+ C.1+ D.2- 解 如图 易知直线AC的方程是y=3.直线AC的方程是＝1.即3x+ 2y=6. 设直线x=a与AB交于D.与AC交于E.则D.E的坐标分别为D(a,3),E(a,) 从而|DE|=3-=a S△ADE＝AD·DE＝a·a=a2 (1) 又S△ABC＝·3·＝. S△ADE＝·S△ACB＝. (2) 由有a2＝.解得a= 应选A. 例16 以A为端点的线段垂直平分线的方程是( ) A.3x-y+8=0 B.3x+y+4=0 C.2x+y+2=0 D.3x+y+8=0 解:设P(x.y)为线段AB的中垂线上的点. 则│PA│=│PB│ 即.化简得3x+y+4= 0. 应选B. 例17 在直角坐标系xoy中.过点P的直线1与直线OP的夹角为45°. 求1的方程. 解:设1的斜率为k.kOP=-. ∴tg45°=││=││=││. 得=±1.解出k=-.7 ∴1的方程为y-4=-. 即1的方程为x+7y-25=0或7x-y+25=0. 例18 点(0.1)到直线x+y=2的距离是 . 解:d= [同步达纲练习] 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•蚌埠模拟）给出下列四个例题，期中正确的命题是（　　）

    查看答案和解析>>

    给出下列四个例题，期中正确的命题是（ ）
    A．各侧面都是正方形的棱柱一定是正棱柱
    B．若直线l⊥平面α，l∥平面β，则α⊥β
    C．若平面α与平面β的交线为m，平面α内的直线n⊥直线m，则直线n⊥平面β
    D．一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面，则这两个二面角的平面角互为补角

    查看答案和解析>>

    给出下列四个例题，期中正确的命题是（ ）
    A．各侧面都是正方形的棱柱一定是正棱柱
    B．若直线l⊥平面α，l∥平面β，则α⊥β
    C．若平面α与平面β的交线为m，平面α内的直线n⊥直线m，则直线n⊥平面β
    D．一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面，则这两个二面角的平面角互为补角

    查看答案和解析>>

    给出下列四个例题，期中正确的命题是


    1. A.
      各侧面都是正方形的棱柱一定是正棱柱
    2. B.
      若直线l⊥平面α，l∥平面β，则α⊥β
    3. C.
      若平面α与平面β的交线为m，平面α内的直线n⊥直线m，则直线n⊥平面β
    4. D.
      一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面，则这两个二面角的平面角互为补角

    查看答案和解析>>

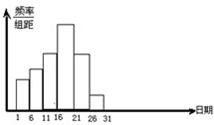    精英家教网在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图），已知从左到右各长方形的高的比为2：3：4：6：4：1，第三组的频数为12，请解答下列问题：
    （1）本次活动共有多少件作品参加评比？
    （2）哪组上交的作品数量最多？共有多少件？
    （3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高？

    查看答案和解析>>


    同步练习册答案