
题目列表(包括答案和解析)
(本题满分12分) 在某次射击比赛中共有5名选手,出场时甲、乙、丙三人不能相邻。求(1)共有多少种不同的出场顺序?
(2)若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
(3)若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5,求三人各射击一
次至少有两人命中目标的概率。
(本小题满分12分)
甲、乙两名射手各进行一次射击,射中环数
 的分布列分别为:
的分布列分别为:
 | 8 | 9 | 10 |
| P | 0.3 | 0.5 | a |
 | 8 | 9 | 10 |
| P | 0.2 | 0.3 | b |
 )确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
)确定a、b的值,并求两人各进行一次射击,都射中10环的概率;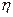 的分布列及期望,并求结束时射击轮次超过2次的概率。
的分布列及期望,并求结束时射击轮次超过2次的概率。
 的分布列分别为:
的分布列分别为: | 8 | 9 | 10 |
| P | 0.3 | 0.5 | a |
 | 8 | 9 | 10 |
| P | 0.2 | 0.3 | b |
 )确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
)确定a、b的值,并求两人各进行一次射击,都射中10环的概率; 的分布列及期望,并求结束时射击轮次超过2次的概率。
的分布列及期望,并求结束时射击轮次超过2次的概率。(本小题满分10分)
某射击小组有甲、乙两名射手,甲的命中率为![]()
![]() ,乙的命中率为
,乙的命中率为![]() ,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.
(Ⅰ)若![]()
![]() ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;
(Ⅱ)计划在2011年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为![]() ,
,
如果![]() ,求
,求![]() 的取值范围;
的取值范围;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com