
题目列表(包括答案和解析)
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.| 5 |
|
|
(本小题满分16分)
高 已知数列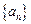 的前
的前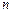 项和为
项和为 ,且满足
,且满足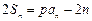 ,
,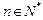 ,其中常数
,其中常数 .
.
(1)证明:数列 为等比数列;
为等比数列;
(2)若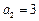 ,求数列
,求数列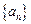 的通项公式;
的通项公式;
(3)对于(2)中数列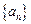 ,若数列
,若数列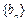 满足
满足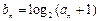 (
(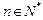 ),在
),在 与
与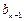 之间插入
之间插入 (
(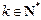 )个2,得到一个新的数列
)个2,得到一个新的数列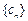 ,试问:是否存在正整数m,使得数列
,试问:是否存在正整数m,使得数列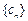 的前m项的和
的前m项的和 ?如果存在,求出m的值;如果不存在,说明理由.
?如果存在,求出m的值;如果不存在,说明理由.
(本小题满分12分)
已知等差数列{an}中a2=8,S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺 序排成一个新数列{bn},试求{bn}的前n项和An.
序排成一个新数列{bn},试求{bn}的前n项和An.
.(本小题满分14分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收
益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单
位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.现
有两个奖励方案的函数模型:(1) ;(2)
;(2) .试问这两个函数模
.试问这两个函数模
型是否符合该公司要求,并说明理由.
(本小题满分12分)
某污水处理厂预计2010年底投入200万元,购入一套污水处理设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加1万元。
(1)求该污水处理厂使用该设备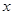 年的年平均费用
年的年平均费用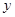 (万元);
(万元);
(2)为使该污水处理厂的年平均费用最低,该污水处理厂几年后需要重新更换新的污水处理设备?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com