设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s(m，n)为所有这样的数表构成的集合。

对于A∈S(m,n),记r_i(A)为A的第ⅰ行各数之和（1≤ⅰ≤m），C_j(A)为A的第j列各数之和（1≤j≤n）：

记K(A)为∣r₁(A)∣,∣R₂(A)∣,…,∣Rm(A)∣,∣C₁(A)∣,∣C₂(A)∣,…,∣Cn(A)∣中的最小值。

（1）   对如下数表A，求K（A）的值；

1	1	-0.8
0.1	-0.3	-1

 

（2）设数表A∈S（2,3）形如

1	1	c
a	b	-1

 

求K（A）的最大值；

（3）给定正整数t，对于所有的A∈S（2,2t+1），求K（A）的最大值。

【解析】（1）因为，

所以

（2）  不妨设.由题意得.又因为，所以，

于是，，

    

所以，当，且时，取得最大值1。

（3）对于给定的正整数t，任给数表如下，

		…
		…

任意改变A的行次序或列次序，或把A中的每一个数换成它的相反数，所得数表

，并且，因此，不妨设，

且。

由得定义知，，

又因为

所以

     

     

所以，

对数表：

1	1	…	1		…
		…		-1	…	-1

 

则且，

综上，对于所有的，的最大值为

 

如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）证明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.

 

【解析】解法一：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0),C(0,1,0), 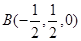,P（0,0,2）.

（1）证明：易得，于是,所以

(2) ,设平面PCD的法向量，

则,即.不防设，可得.可取平面PAC的法向量于是从而.

所以二面角A-PC-D的正弦值为.

（3）设点E的坐标为（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）证明：由，可得，又由,,故.又,所以.

(2)如图，作于点H，连接DH.由,,可得.

因此,从而为二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值为.

（3）如图，因为，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF. 故或其补角为异面直线BE与CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.

 

学数学，是要使人聪明，思维更加缜密.目前在美国广为流传的一道数学题是——老板给了两个加工资的方案：一是每年年末比上一年增加一千元；二是每半年结束时加300元，请选一种.不擅数学的，很容易选择前者：一年加一千元总比两个半年共加600元要多.其实，由于加工资是累计的，时间稍长，往往第二种方案更有利.例如，在第三年的年末，依第一种方案可加1 000+2 000+3 000=6 000元；第二种方案可加300+600+900+1 200+1 500+1 800=6 300元，比第一种方案多了300元.第四年、第五年会多得更多.因此，你若会在该公司干三年以上(包括三年)，应选择第二种方案.

由以上材料，再来解答下列问题：

(1)若在该公司干10年，则选择第二种方案比选择第一种方案多加薪多少元？

(2)若把第二种方案中的“每半年加300元”改为“每半年加a元”，问a取何值时，选择第二种方案总比选择第一种方案多加薪(假设工作时间是整年数)？

若方程x²＋(m－2)x－m＋5＝0的两个根都大于2，求实数m的取值范围．

阅读下面的解法，回答提出的问题．

解：第一步，令判别式Δ＝(m－2)²－4(－m＋5)≥0，

解得m≥4或m≤－4；

第二步，设两根为x₁，x₂，由x₁＞2，x₂＞2得

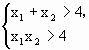，所以．

所以m＜－2．

第三步，由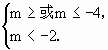得m≤－4．

第四步，由第三步得出结论．

当m∈(－∞，－4]时，此方程两根均大于2．

但当取m＝－6检验知，方程x²－8x＋11＝0两根为x＝4±，其中4－＜2．

试问：产生错误的原因是什么？

已知函数f(x)=e^x-ax，其中a＞0.

（1）若对一切x∈R，f(x) 1恒成立，求a的取值集合；

（2)在函数f(x)的图像上去定点A（x₁, f(x₁)）,B(x₂, f(x₂))(x₁<x₂)，记直线AB的斜率为k，证明：存在x₀∈（x₁,x₂）,使恒成立.

【解析】解：令.

当时单调递减；当时单调递增，故当时，取最小值

于是对一切恒成立，当且仅当.　　　　　　　　①

令则

当时，单调递增；当时，单调递减.

故当时，取最大值.因此，当且仅当时，①式成立.

综上所述，的取值集合为.

（Ⅱ）由题意知，令则

令，则.当时，单调递减；当时，单调递增.故当，即

从而，又

所以因为函数在区间上的图像是连续不断的一条曲线，所以存在使即成立.

【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出取最小值对一切x∈R，f(x) 1恒成立转化为从而得出求a的取值集合；第二问在假设存在的情况下进行推理，然后把问题归结为一个方程是否存在解的问题，通过构造函数，研究这个函数的性质进行分析判断.