（本小题满分12分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据

 (1)请画出上表数据的散点图； (2)请根据上表提供的数据，用最小二乘法求出Y关于x的线性回归方程Y=bx+a；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

  (参考数值：32．5+43+54+64．5=66.5)

（本小题满分12分）

某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如图1；B产品的利润与投资的算术平方根成正比，其关系如图2(注：利润和投资单位：万元)．

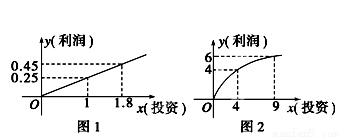
(1)分别将A、B两种产品的利润表示为投资的函数关系式；

(2)已知该企业已筹集到18万元资金，并将全部投入A，B两种产品的生产．

①若平均投入生产两种产品，可获得多少利润？

②问：如果你是厂长，怎样分配这18万元投资，才能使该企业获得最大利润？其最大利润约为多少万元？

（本小题满分12分）

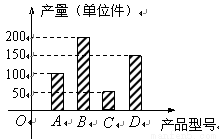
某工厂2011年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加四月份的一个展销会：

   （1）问A、B、C、D型号的产品各抽取多少件？

   （2）从A、C型号的产品中随机的抽取3件，用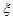表示抽取A种型号的产品件数，求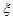的分布列和数学期望。

（本小题满分12分）

某汽车配件厂生产A、B两种型号的产品，A型产品的一等品率为，二等品率为；B型产品的一等品率为，二等品率为。生产1件A型产品，若是一等品则获得4万元利润，若是二等品则亏损1万元；生产1件B型产品，若是一等品则获得6万元利润，若是二等品则亏损2万元。设生产各件产品相互独立。

（1）求生产4件A型产品所获得的利润不少于10万元的概率；

（2）记(单位：万元)为生产1件A型产品和1件B型产品可获得的利润，求的分布列及期望值.

（本小题满分12分）
某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如图1；B产品的利润与投资的算术平方根成正比，其关系如图2(注：利润和投资单位：万元)．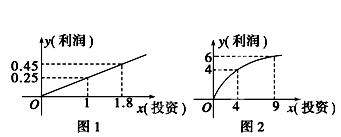

(1)分别将A、B两种产品的利润表示为投资的函数关系式；
(2)已知该企业已筹集到18万元资金，并将全部投入A，B两种产品的生产．
①若平均投入生产两种产品，可获得多少利润？
②问：如果你是厂长，怎样分配这18万元投资，才能使该企业获得最大利润？其最大利润约为多少万元？