题目列表(包括答案和解析)
如图，在斜三棱柱ABC－A1B1C1中，∠A1AB＝∠A1AC，AB＝AC，侧面B1BCC1与底面ABC所成的二面角为120°，E、F分别是棱CB1、AA1的中点．
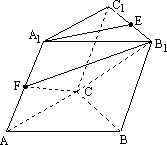
(1)AA1求与底面ABC所成的角；
(2)证明EA1∥平面B1FC；
如下图，在斜三棱柱ABC－A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°
的角，AA1＝2，底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且BE＝
BC1．
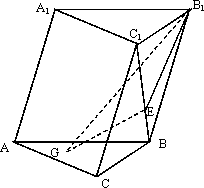
(1)求证：GE∥侧面AA1B1B；
(2)求平面B1GE与底面民ABC所成锐二面角的大小．
如图，在斜三棱柱ABC－A1B1C1 中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成600的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点．E是线段BC1上一点，且BE=
BC1．
(1)求证：GE∥侧面AA1B1B；
(2)求平面B1GE与底面ABC所成锐二面角的大小
如图，点P为斜三棱柱ABC－A1B1C1的侧棱BB1上一点，PM⊥BB1交AA1于点M，PN⊥BB1交CC1于点N.
(1)求证：CC1⊥MN.
(2)在任意△DEF中，
有由余弦定理DE2＝DF2＋EF2－2DF·EFcos∠DFE，拓展到空间，类比三角形的余弦定理，写出一个斜三棱柱的三个侧面积与其中两个侧面所成的二面角之间的关系式，并加以证明．
如图，各棱长都等于2的斜三棱柱ABC－A1B1C1中，侧面ABB1A1垂直于底面．
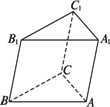
(1)侧棱与底面所成角为多少时，能使B1C⊥AC1；
(2)在(1)的条件下求此三棱柱的侧面积．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com