
题目列表(包括答案和解析)
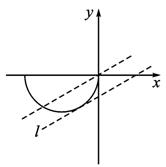
(1)试问点P的轨迹是什么曲线?
(2)已知直线l的斜率为![]() ,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
如图,已知过原点O从x轴正方向出发顺时针转60°得到射线t,点A(x,y)在射线t上![]() x>0,y<0
x>0,y<0![]() ,设|OA|=m;又点B(
,设|OA|=m;又点B(![]() ,
,![]() )在射线y=0(
)在射线y=0(![]() >0)上移动;设点P为第四象限的动点,若
>0)上移动;设点P为第四象限的动点,若![]() ·
·![]() =0,且
=0,且![]() ·
·![]() ,
,![]()
![]() ·
·![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求动点P的轨迹方程,并说明轨迹C的形状;
(Ⅱ)已知动直线l与曲线C有三个不同的交点M、N,且![]() ∥v,v=(2,1),设 Q(
∥v,v=(2,1),设 Q(![]() ,
,![]() )为线段MN的中点,求
)为线段MN的中点,求![]() 的取值范围.
的取值范围.

(Ⅰ)求动点P的轨迹方程,并说明轨迹C的形状;
(Ⅱ)已知动直线l与曲线C有三个不同的交点M、N,且![]() ∥v,v=(2,1),设 Q(
∥v,v=(2,1),设 Q(![]() ,
,![]() )为线段MN的中点,求
)为线段MN的中点,求![]() 的取值范围.
的取值范围.

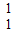 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.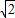 sin(
sin(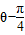 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为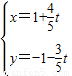 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.
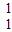 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.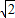 sin(
sin(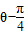 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为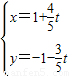 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com