三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．

(17)（本小题满分12分）

已知函数．

(I)求函数的最小正周期；

(Ⅱ)当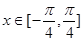时，函数的最小值为，求实数的值．

 

₁₇（本小题满分12分）

设等差数列满足，。

（Ⅰ）求的通项公式；

（Ⅱ）求的前项和及使得最大的序号的值。

 

（本小题满分12分）首届世界低碳经济大会11月17日在南昌召开，本届大会以“节能减排，绿色生态”为主题。某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本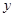（元）与月处理量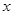（吨）之间的函数关系可近似的表示为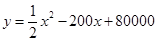：，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．

（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？

（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？

 

 

(本小题满分14分)

某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:

序      号	1	2	3	4	5	6	7	8	9	10
身高x(厘米)	192	164	172	177	176	159	171	166	182	166
脚长y( 码 )	48	38	40	43	44	37	40	39	46	39
序      号	11	12	13	14	15	16	17	18	19	20
身高x(厘米)	169	178	167	174	168	179	165	170	162	170
脚长y( 码 )	43	41	40	43	40	44	38	42	39	41

(Ⅰ)若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的联列表:

	高  个	非高个	合  计
大  脚
非大脚		12
合  计			20

   (Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?

   (Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:

①抽到12号的概率；②抽到“无效序号(超过20号)”的概率.

三、解答题(本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤)

17．（本题满分10分）

已知向量, 的夹角为, 且, , 若, , 求（1）·；

（2）.