（本题10分） 为了解高二学年女生身高情况，对高二(10)班女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：

组　别	频数	频率
145.5～149.5	1	0.02
149.5～153.5	4	0.08
153.5～157.5	20	0.40
157.5～161.5	15	0.30
161.5～165.5	8	0.16
165.5～169.5	m	n
合　计	M	N

（1）求出表中所表示的数分别是多少？

（2）若该校高二学年共有女生500人，试估计高二女生中身高在161.5以上的人数。

 

（本题10分） 为了解高二学年女生身高情况，对高二(10)班女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：

组　别	频数	频率
145.5～149.5	1	0.02
149.5～153.5	4	0.08
153.5～157.5	20	0.40
157.5～161.5	15	0.30
161.5～165.5	8	0.16
165.5～169.5	m	n
合　计	M	N

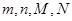（1）求出表中所表示的数分别是多少？
（2）若该校高二学年共有女生500人，试估计高二女生中身高在161.5以上的人数。

(本题满分12分)

某学校的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
数学	95	75	80	94	92	65	67	84	98	71	67	93	64	78	77	90	57	83	72	83
物理	90	63	72	87	91	71	58	82	93	81	77	82	48	85	69	91	61	84	78	86

若单科成绩在85分以上(含85分)，则该科成绩为优秀．

（1）根据上表完成下面的列联表（单位：人）

	数学成绩优秀	数学成绩不优秀	总计
物理成绩优秀
物理成绩不优秀
总计			20

（2）根据（1）中表格的数据计算，是否有99%的把握，认为学生的数学成绩与物理成绩之间有关系？

（3）若从这20个人中抽出1人来了解有关情况，求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率．

参考公式:

P(K2≥k)	0.100	0.050	0.025	0.010	0.001
k	2.706	3.841	5.024	6.635	10.828

(本小题满分10分)

某食品公司为了解某种新品种食品的市场需求，进行了20天的测试，人为地调控每天产品的单价P(元/件)：前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表：

时间(将第x天记为x) x	1	10	11	18
单价(元/件)P	9	0	1	8

而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.

(1)写出每天销售y(元)与时间x(天)的函数关系式y=f(x);

(2)在这20天中哪一天销售收入最高？为使每天销售收入最高,按此测试结果应将单价P设定为多少元为好?(结果精确到1元)

 

（本小题满分12分）甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：

 

分组	[70,80）	[80,90）	[90,100）	[100,110）
频数	3	4	8	15
分组	[110,120）	[120,130）	[130,140）	[140,150]
频数	15	x	3	2

    甲校：

 

 

分组	[70,80）	[80,90）	[90,100）	[100,110）
频数	1	2	8	9
分组	[110,120）	[120,130）	[130,140）	[140,150]
频数	10	10	y	3

    乙校：

 

 

 

（Ⅰ）计算x，y的值。

（Ⅱ）若规定考试成绩在[120,150]内为优秀，请分别估计两个学校数学成绩的优秀率。

 

	甲校	乙校	总计
优秀
非优秀
总计

 

 

 

 

 

 

（Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异。

参考数据与公式：

由列联表中数据计算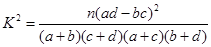

临界值表