（本小题满分13分）

　　甲和乙参加智力答题活动，活动规则：①答题过程中，若答对则继续答题；若答错则停止答题；②每人最多答3个题；③答对第一题得10分，第二题得20分，第三题得30分，答错得0分。已知甲答对每个题的概率为，乙答对每个题的概率为。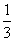

　　（1）求甲恰好得30分的概率；

　　（2）设乙的得分为，求的分布列和数学期望；

　　（3）求甲恰好比乙多30分的概率.

（本小题满分13分）

　　已知：如图，长方体中，、分别是棱,上的点，,.

　　（1） 求异面直线与所成角的余弦值；

　　（2） 证明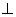平面；

　　（3） 求二面角的正弦值.

（本小题共13分）

　　一厂家向用户提供的一箱产品共10件，其中有2件次品，用户先对产品进行抽检以决定是否接收。抽检规定是这样的：一次取一件产品检查，若前三次没有抽查到次品，则用户接收这箱产品，而前三次中只要抽查到次品就停止抽检，并且用户拒绝接收这箱产品。

　　（I）求这箱产品被用户拒绝接收的概率；

　　（II）记表示抽检的产品件数，求的概率分布列。

（本小题共14分）

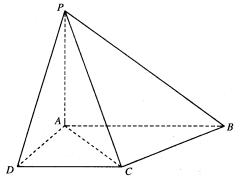
　　四棱锥P—ABCD中，PA⊥底面ABCD，AB//CD，AD=CD=1，∠BAD=120°，PA=，∠ACB=90°。

　　（I）求证：BC⊥平面PAC；

　　（II）求二面角D—PC—A的大小；

　　（III）求点B到平面PCD的距离。

（本小题共13分）

　　如图，在直角坐标系中，O为坐标原点，直线AB⊥x轴于点C，，动点M到直线AB的距离是它到点D的距离的2倍。

　　（I）求点M的轨迹方程；

　　（II）设点K为点M的轨迹与x轴正半轴的交点，直线l交点M的轨迹于E，F两点（E，F与点K不重合），且满足，动点P满足，求直线KP的斜率的取值范围。