
题目列表(包括答案和解析)
阅读理解:对于任意正实数a、b,∵ ≥0,∴
≥0,∴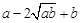 ≥0,
≥0,
∴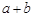 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在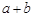 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为 ,考虑何时时周长
,考虑何时时周长 最小。
最小。
∵m>0,  (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.

| |||||
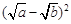 ≥0,∴
≥0,∴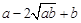 ≥0,
≥0,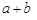 ≥
≥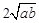 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.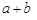 ≥
≥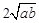 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥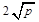 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值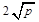 .
.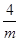 ,考虑何时时周长
,考虑何时时周长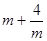 最小。
最小。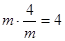 (定值),由以上结论可得:
(定值),由以上结论可得: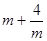 有最小值是 ;
有最小值是 ;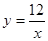 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.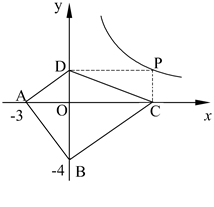
阅读下列材料:
任意给定一个矩形ABCD,一定存在另一个矩形![]() ,使它的周长和面积分别是矩形ABCD周长和面积的k倍(k≥2,且k是整数).我们把矩形
,使它的周长和面积分别是矩形ABCD周长和面积的k倍(k≥2,且k是整数).我们把矩形![]() 叫做矩形ABCD的k倍矩形.
叫做矩形ABCD的k倍矩形.
例:矩形ABCD的长和宽分别为3和1,它的周长和面积分别为8和3;矩形![]() 的长和宽分别为4+
的长和宽分别为4+![]() 和4-
和4-![]() ,它的周长和面积分别为16和6.这时,矩形
,它的周长和面积分别为16和6.这时,矩形![]() 的周长和面积分别是矩形ABCD周长和面积的2倍,则矩形
的周长和面积分别是矩形ABCD周长和面积的2倍,则矩形![]() 叫做矩形ABCD的2倍矩形.
叫做矩形ABCD的2倍矩形.
解答下列问题:
(1)填空:一个矩形的周长和面积分别为10和6,则它的2倍的矩形的周长为________,面积为________;
(2)已知矩形ABCD的长和宽分别为2和1,那么是否存在它的k倍矩形![]() ,使
,使![]() ∶AB=
∶AB=![]() ∶BC?若存在,请求出k的值;若不存在,请说明理由.
∶BC?若存在,请求出k的值;若不存在,请说明理由.
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
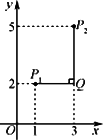
(1)已知点A(-![]() ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
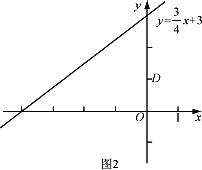
(2)已知C是直线y=![]() x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
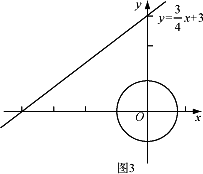
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E和点C的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com