
题目列表(包括答案和解析)
如图16,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形。
(1)求证:AB∥CQ;
(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并给予证明;若AQ与CQ不能互相垂直,请说明理由。
 |

 有红、黄、绿三块面积均为20cm2的正方形纸片,放在一个底面是正方形的盒子内,它们之间互相叠合(如图),已知露在外面的部分中,红色纸片面积是20cm2,黄色纸片面积是14cm2,绿色纸片面积是10cm2,那么正方形盒子的底面积是( )
有红、黄、绿三块面积均为20cm2的正方形纸片,放在一个底面是正方形的盒子内,它们之间互相叠合(如图),已知露在外面的部分中,红色纸片面积是20cm2,黄色纸片面积是14cm2,绿色纸片面积是10cm2,那么正方形盒子的底面积是( ) ABCD中,AE=CF,M、N分别是DE、BF的中点.
ABCD中,AE=CF,M、N分别是DE、BF的中点.
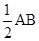 ,求∠APB的度数.
,求∠APB的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com