
题目列表(包括答案和解析)
在平面直角坐标系中,圆M∶(x-1)2+(y-1)2=5在点A(3,2)处的切线方程可如下求解:设P(x,y)为切线上任一点,则由向量方法可得切线方程为:2x+y-8=0,类似地,在空间直角坐标系中,球M∶(x-1)2+(y-1)2+(z-1)2=6在点A(3,2,2)处的切面方程为________.
设不等边三角形ABC的外心与重心分别为M、G,若A(-1,0),B(1,0)且MG//AB.
(Ⅰ)求三角形ABC顶点C的轨迹方程;
(Ⅱ)设顶点C的轨迹为D,已知直线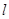 过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线
过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线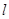 的方程.
的方程.
【解析】
第一问因为设C(x,y)(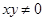 )
)
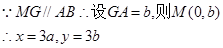 ……3分
……3分
∵M是不等边三解形ABC的外心,∴|MA|=|MC|,即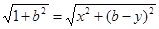 (2)
(2)
由(1)(2)得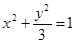 .所以三角形顶点C的轨迹方程为
.所以三角形顶点C的轨迹方程为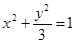 ,
,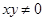 .…6分
.…6分
第二问直线l的方程为y=kx+1
由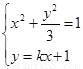 消y得
消y得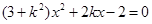 。 ∵直线l与曲线D交于P、N两点,∴△=
。 ∵直线l与曲线D交于P、N两点,∴△=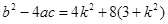 ,
,
又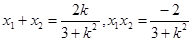 ,
,
∵ ,∴
,∴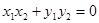
 得到直线方程。
得到直线方程。
已知函数f(x)=![]() x3-x2+ax+b的图像在点P(0,f(0))处的切线方程为y=3x-2
x3-x2+ax+b的图像在点P(0,f(0))处的切线方程为y=3x-2
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+![]() 是[2,+∞]上的增函数.
是[2,+∞]上的增函数.
(ⅰ)求实数m的最大值;
(ⅱ)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
(Ⅰ)将两圆方程相减可得一直线方程l:x+y-4=0,该直线叫做这两圆的“根轴”,试证点P落在根轴上;
(Ⅱ)求切线长|PA|的最小值;
 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com