
题目列表(包括答案和解析)
设事件A发生的概率为p(0<p<1),
(1)证明事件A在一次试验中发生次数ε的方差不超过![]() .
.
(2) 求![]() 的最大值
的最大值
(3)在n次独立重复实验中,事件A发生次数ξ的方差最大值是多少?
在一次实验中,事件A发生的概率是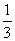 ,在n次独立重复实验中,事件A至少发生一次的概率是不少于
,在n次独立重复实验中,事件A至少发生一次的概率是不少于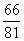 ,则n的最小值是____________.
,则n的最小值是____________.
(理)在一次实验中,事件A发生的概率为p(0<p<1),设在k次独立重复实验中,事件A发生k次的概率记为pk,则![]() =
=
A.1
B.1-(1-p)n
C.p![]()
D.np
如果在一次试验中,某事件A发生的概率为p,那么在n次独立重复试验中,这件事A发生偶数次的概率为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com