已知命题p：“∀x∈[0，1]，a≥ex”，命题q：“∃x∈R，x2＋4x＋a＝0”，若命题“p∧q”是真命题；则实数a的取值范围是(　　)

A．(4，＋∞)          B．[1，4]         C．[e，4]              D．(－∞，1]

已知命题p：“∀x∈[1,2]，x²－a≥0”，命题q：“∃x∈R”，x²＋2ax＋2－a＝0，若命题“p∧q”是真命题，则实数a的取值范围是(　　)

A．a≤－2或a＝1          B．a≤－2或1≤a≤2

C．a≥1                   D．－2≤a≤1

已知命题p：“∀x∈[1,2]，x²－a≥0”，命题q：“∃x∈R”，x²＋2ax＋2－a＝0，若命题“p∧q”是真命题，则实数a的取值范围是(　　)

A．a≤－2或a＝1       B．a≤－2或1≤a≤2

C．a≥1                D．－2≤a≤1

已知命题p：∀x∈R，sin x≤1，则(　　)

A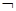． p：∃x₀∈R，sin x₀≥1

B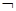． p：∀x∈R，sin x≥1

C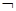． p：∃x₀∈R，sin x₀>1

D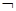． p：∀x∈R，sin x>1

已知命题p：“∀x∈[1，2]，x²－a≥0”，命题q：“∃x₀∈R，x₀²＋2ax₀＋2－a＝0”，若命题“p且q”是真命题，则实数a的取值范围是________．