（12分）某农产品去年各季度的市场价格如下表：

季度	第一季度	第二季度	第三季度	第四季度
每吨售价（单位：元）	195.5	200.5	204.5	199.5

今年某公司计划按去年各季度市场价格的“平衡价”（ 平衡价是这样的一个量：与上年各季度售价差比较，与各季度售价差的平方和最小）收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购万吨，政策为了鼓励收购公司多收购该种农产品，决定将税率降低个百分点，预测收购量可增加个百分点。

（1）求

（2）写出税收（万元）与的函数关系式，

（3）若要使此项税收在税率调节后不少于原计划税收的83.2%，试确定的范围。

某省环保研究所对市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数与时刻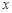(时) 的关系为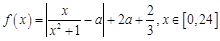，其中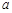是与气象有关的参数，且．

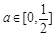（1）令, 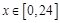，写出该函数的单调区间，并选择其中一种情形进行证明；

（2）若用每天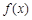的最大值作为当天的综合放射性污染指数，并记作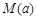，求；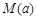

（3）省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？

【解析】第一问利用定义法求证单调性，并判定结论。

第二问（2）由函数的单调性知，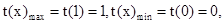

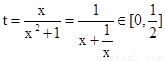∴，即t的取值范围是． 

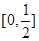当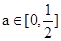时，记

则 

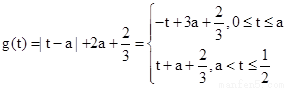
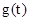∵在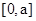上单调递减，在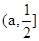上单调递增，

第三问因为当且仅当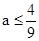时，.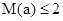

故当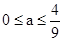时不超标，当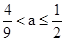时超标．