设函数y＝f(x)是定义在R上的函数，并且满足下面三个条件：

(1)对任意正数x、y，都有f(xy)＝f(x)＋f(y)；

(2)当x＞1时，f(x)＜0；

(3)f(3)＝－1．

(Ⅰ)求的值；

(Ⅱ)证明f(x)在R⁺上是减函数；

(Ⅲ)如果不等式f(x)＋f(2－x)＜2成立，求x的取值范围；

(Ⅳ)如果存在正数k，使不等式f(kx)＋f(2－x)＜2有解，求正数k的取值范围．

设函数y＝f(x)的定义如下表，数列{x_n}满足x₀＝5，对任意自然数n均有x_n+1＝f(x_n)，则x₂₀₀₇的值为

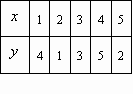
A．1

B．2

C．4

D．5

设函数y＝f(x)是定义在R₊上的函数，并且满足下面三个条件：(1)对任意正数x、y都有f(xy)＝f(x)＋f(y)；(2)当x＞1时，f(x)＜0；(3)f(3)＝－1

(Ⅰ)求f(1)和f()的值；

(Ⅱ)如果不等式f(x)＋f(2－x)＜2成立，求x的取值范围．

(Ⅲ)如果存在正数k使不等式f(kx)＋f(2－x)＜2有解，求正数k的取值范围．

设函数y＝f(x)是定义在R上的函数，并且满足下面三个条件：

①对任意正数x、y，都有f(xy)＝f(x)＋f(y)；②当x＞1时，f(x)＜0；③f(3)＝－1．

(Ⅰ)求的值；

(Ⅱ)如果不等式f(x)＋f(2－x)＜2成立，求x的取值范围；

(Ⅲ)如果存在正数k，使不等式f(kx)＋f(2－x)＜2有解，求正数k的取值范围．