
题目列表(包括答案和解析)
如图,正方体ABCD-A1B1![]() C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为 .
C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为 .
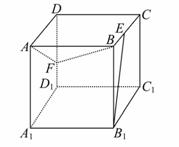
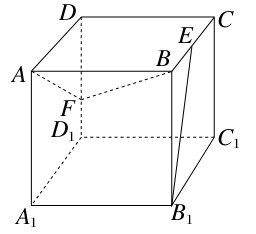
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的和的值为________.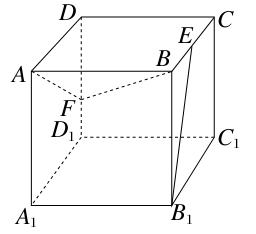
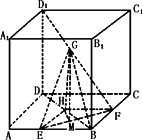
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别在棱AB、BC上,G在对角线BD1上,且AE=![]() ,BF=
,BF=![]() ,D1G∶GB=1∶2,求平面EFG与底面ABCD所成的二面角的大小.
,D1G∶GB=1∶2,求平面EFG与底面ABCD所成的二面角的大小.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=,则下列结论中错误的是 ( )
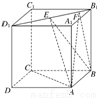
A.AC⊥BE B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值 D.△AEF的面积与△BEF的面积相等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com