练习册

  • 练习册
  • 试题
    填空. 如图:连接BC ∵AB//CD ∴ = 又∠1=∠2 ∴∠FBC=∠BCE ∴ // ∴∠E=∠F 【查看更多】

     

    题目列表(包括答案和解析)

    问题情境

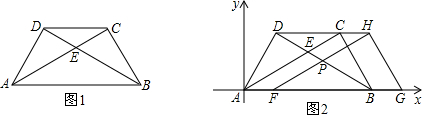
    　　　 如图，在轴上有两点,（）.分别过点，点作轴的垂线，交抛物线于点、点.直线交直线于点，直线交直线于点,点、点的纵坐标分别记为、.

    特例探究

    填空：

    当,时，=____,=______.当,时，=____,=______.

    归纳证明

    对任意,（）,猜想与的大小关系，并证明你的猜想

    拓展应用.

    （1）　　　 若将“抛物线”改为“抛物线”,其它条件不变，请直接写出与的大小关系.

    （2）　　　 连接，．当时，直接写出和的关系及四边形的形状．

    [

    查看答案和解析>>

    完成推理填空：如图所示，已知AD=BC，AB=DC，试判断∠A与∠ABC的关系．下面是小颖同学的推导过程：
    解：连接BD．在△ABD与△CDB中
    ∵AD=CB　　　　 （已知）
    AB=CD　　　　 （已知）
    BD=DB　　　　　（________）
    ∴△ABD≌△CDB　 （________）
    ∴∠1=∠2　　　　（________）
    ∴AD∥BC　　　　 （________）
    ∴∠A+∠ABC=180°（________）

    查看答案和解析>>

    如图1-3是由边长为1的小正方形组成的网格，点A、B、C、D都在网格的格点上，AC、BD相交于点O．

    （1）填空：如图1，当AB=2，连接AD．tan∠AOD=
    3
    3
    ；如图2，当AB=3，画AH⊥BD交BD的延长线于H点，则AH=
    3
    		2
    2
    3
    		2
    2
    ，tan∠AOD=
    2
    2
    ；如图3，当AB=4，tan∠AOD=
    5
    3
    5
    3
    ；
    （2）猜想：当AB=n（n＞0）时，tan∠AOD=
    n+1
    n-1
    n+1
    n-1
    ；（结果用含有n的代数式表示）．请证明你的结论；
    （3）如图4．两个正方形的一边CD、CG在同一直线上，连接CF、DE相交于点O，若tan∠COE=
    19
    6
    ．求正方形ABCD与正方形CEFG的边长之比．

    查看答案和解析>>

    将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连接CD．
    精英家教网
    （1）填空：如图1，AC=
     
    ，BD=
     
    ；四边形ABCD是
     
    梯形；
    （2）请写出图1中所有的相似三角形；（不含全等三角形）
    （3）如图2，若以AB所在直线为轴，过点A垂直于AB的直线为轴建立如图2的平面直角坐标系，保持△ABD不动，将△ABC向x轴的正方向平移到△FGH的位置，FH与BD相交于点P，设AF=t，△FBP面积为S，求S与t之间的函数关系式，并写出t的取值范围．

    查看答案和解析>>

    按要求画图并填空：如图，已知三角形ABC及点D，CB⊥AB，B为垂足．
    （1）作直线AD；
    （2）延长AB到E，使得BE=AB，连接CE；
    （3）作射线DE；
    （4）图中线段
    CB
    CB
    的长表示点C到线段AE所在直线的距离．

    查看答案和解析>>


    同步练习册答案