
题目列表(包括答案和解析)
5、圆内接四边形ABCD的内角∠A:∠B:∠C=2:3:4,则∠D=________°
4、方程 x 2 = x 的解是__________________
3、如图,要给这个长、宽、高分别为x、y、z的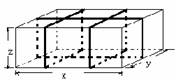 箱子打包,其打包方式如右图所示,则打包带的长至少要_________ (单位:mm)(用含x、y、z的代数式表示)
箱子打包,其打包方式如右图所示,则打包带的长至少要_________ (单位:mm)(用含x、y、z的代数式表示)
2、据有关资料显示,长江三峡工程电站的总装机容量是18200000千瓦,请你用科学记数法表示电站的总装机容量,应记为 千瓦
1、已知点P(-2,3),则点P关于x轴对称的点坐标是( )
29.解:(1)过点D作DE//AC交BC的延长线于点E,又∵AD//BC,
∴四边形ACED为平行四边形,
∴AD=CE,DE=AC,
又∵AD//BC,∴S△ABD=S△DCE,
∵AC⊥BD,DE//AC,
∴DE⊥BD,
∴S梯形ABCD=SRt△BDE=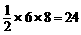 (cm2);
(cm2);
(2)本题中可以减少条件“AD//BC”,同样能求出四边形ABCD的面积S,且求得结果与第(1)小题相同.
∵AC⊥BD,∴S△ABD=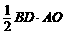 ,S△BCD=
,S△BCD=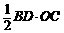 ,
,
∴S四边形ABCD= S△ABD+ S△BCD =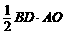 +
+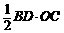 =
=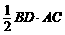 =
=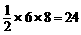 (cm2).
(cm2).
另解:(1)设OA=x,则OC=8-x,
∵AC⊥BD,
∴S梯形ABCD=S△ABD+S△BCD=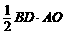 +
+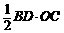 =
=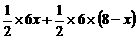 =
=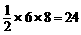 (cm2).
(cm2).
(2)减少条件“AD//BC”
28. (1)两张纸片的重叠部分面积不一定会保持不变.应增加条件“扇形纸片的圆心角∠DOE为120°”,
(1)两张纸片的重叠部分面积不一定会保持不变.应增加条件“扇形纸片的圆心角∠DOE为120°”,
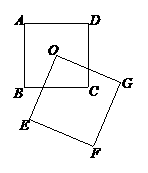
简证如下:连结OB、OC,因为点O是等边△ABC的中心,所以OB、OC为角平分线,且OB=OC,可证△OGB≌△OCF,从而重叠部分面积等于△OBC的面积,即等于等边△ABC的面积的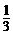 (定值).
(定值).
(2)由这一游戏,还能联想到如图所示的两个正方形:点O为正方形ABCD的对称中心,另一正方形OEFG绕点O旋转过程中,两个正方形的重叠部分面积保持不变,总是正方形ABCD的面积的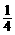 .
.
27.解:(1)若抛物线y=x2-(a+2)x+9的顶点在y轴上,由顶点的横坐标为0,得a=2;若抛物线y=x2-(a+2)x+9的顶点在x轴上,由△=0得a=4或a=-8.
(2)根据题意得a=4,此时抛物线为y=x2-6x+9.解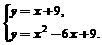 得
得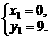
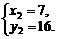 所以A(0,9)、B(7,16).
所以A(0,9)、B(7,16).
①由于点P在上y=x+9上,因此设符合题意的点P的坐标为(t,t+9),此时对应的点Q的坐标为(t,t2-6t+9),由题意得PQ=(t+9) -(t2-6t+9)=6,解得t=1或6,由题意0<t<7,点P的坐标为(1,10)或(6,15);
②设在线段AB上是否存在这样的点P,使得△ABQ∽△OAC,∴∠BAQ=∠AOC=90°,分别过B、Q两点向y轴作垂线,垂足为E、H,由∠BAQ=90°,注意到直线y=x+9与x轴所夹的锐角为45°,由QH=AH可求得点Q的坐标为(5,4),但显然AB∶AQ≠OA∶OC,∴△ABQ与△OAC不可能相似,∴若线段AB上不存在符合条件的点P.
26.(1)14%;
(2)60-79;
(3)如“样本中在60分以下(不含60分)的有105人”,“样本中没获奖的占大多数,达到86%”等;
(4)可能事件.
25.(1)设每千克应涨价x元,则(10+x)(500-20x)=6000
解得x=5或x=10,为了使顾客得到实惠,所以x=5.
(2)设涨价x元时总利润为y,
则y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125
当x=7.5时,y取得最大值,最大值为6125.
答:(1)要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克应涨价5元;(2)若该商场单纯从经济角度看,每千克这种水果涨价7.5元,能使商场获利最多.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com