
题目列表(包括答案和解析)
5.设全集为R,集合E=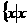 <4或x>6
<4或x>6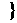 ,F=
,F=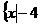 <x<4
<x<4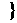 ,则
,则
A.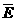 ∪F=R
B.E∪
∪F=R
B.E∪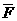 =R
C.
=R
C.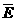 ∪
∪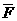 =R
D.E∪F=R
=R
D.E∪F=R
4.实数a、b、c满足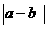 <
< ,则下列不等式中成立的是
,则下列不等式中成立的是
A.a>b-c B.a<b+c
C. >
>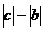 D.
D. <
<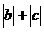
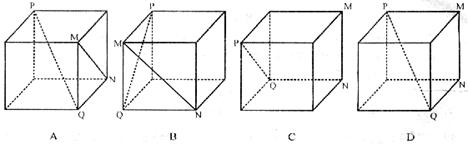
3.在下列四个正方体中,能得出PQ⊥MN的是
2.[理]极坐标平面内,定点P(1,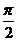 )到曲线
)到曲线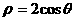 上的点的最短距离是
上的点的最短距离是
A. 1
B.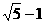 C.
C.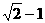 D.
D.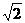
[文]已知点P(0,1),M是圆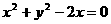 上任意一点,则|PM|的最小值是
上任意一点,则|PM|的最小值是
A.1
B.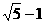 C.
C.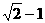 D.
D.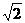
1.已知函数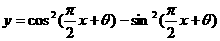 在x=2时有最小值,则
在x=2时有最小值,则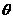 的一个值是
的一个值是
A. 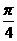 B.
B.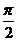 C.
C.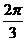 D.
D.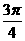
22.(本小题满分14分)
已知抛物线y=-x2+ax+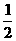 与直线y=2x
与直线y=2x
(1)求证:抛物线与直线相交
(2)求当抛物线的顶点在直线下方时,a的取值范围
(3)当a在(2)的取值范围时,求抛物线截直线所得弦长的最小值
21.(本小题满分12分)
从材料工地运送电线杆到500m以外的公路一方安装,每隔50m在路边要装一根。又知每次只能运三根,要完成运输20根电线杆,并返回材料工地,问运输卡车共行路程多少公里?
20.(本小题满分12分)
在底面是等腰直角三角形的直三棱柱ABC-A1B1C1中,∠C=90°,AA1=AC,D是CC1的中点。
(1)求证:平面AB1D⊥平面AB1B
(2)求二面角 B-B1D-A的正切值
19.(本小题满分12分)
设函数f(x)=x2-2x+2,x∈[ t,t+1]的最小值为g(t),求g(t)的表达式。
18.(本小题满分12分)
甲、乙、丙三人去破译一个密码,他们能译出密码的概率分别为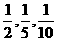 。试求:
。试求:
(1)恰有一人译出密码的概率
(2)密码能破译出的概率
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com