
题目列表(包括答案和解析)
59、集合P=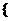 1,3,5,7,9,┅,2
1,3,5,7,9,┅,2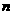 -1,┅
-1,┅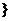
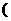
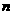 ∈N
∈N
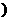 ,若
,若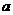 ∈P,
∈P,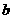 ∈P时,
∈P时,
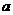
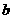 ∈P,则运算 可能是(
D )
∈P,则运算 可能是(
D )
(A)加法; (B)除法; (C)减法; (D)乘法.
58、歌德巴赫(Goldbach.C.德.1690-1764)曾研究过“所有形如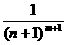 (
( ,
,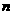 为正整数)的分数之和”问题.为了便于表述,引入记号:
为正整数)的分数之和”问题.为了便于表述,引入记号:
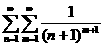 =
=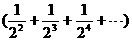 +
+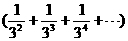 +┅
+┅
+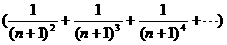 +┅
+┅
写出你对此问题的研究结论: 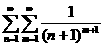 =1 (用数学符号表示).
=1 (用数学符号表示).
57、已知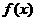 是定义在
是定义在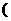 -∞,+∞
-∞,+∞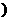 上的函数,
上的函数, ∈
∈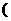 -∞,+∞
-∞,+∞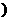 ,请给出能使命题:“若
,请给出能使命题:“若 +1>0,则
+1>0,则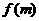 +
+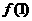 >
>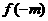 +
+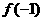 ”成立的一个充分条件:
”成立的一个充分条件:
.
已知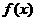 是定义在
是定义在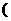 -∞,+∞
-∞,+∞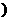 上的函数,
上的函数, ∈
∈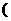 -∞,+∞
-∞,+∞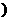 ,请给出能使命题:“若
,请给出能使命题:“若 +1>0,则
+1>0,则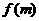 +
+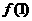 >
>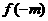 +
+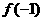 ”成立的一个充分条件:_______.
”成立的一个充分条件:_______.
答案: 函数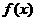 在
在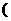 -∞,+∞
-∞,+∞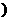 上单调递增(或
上单调递增(或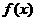 =
=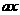 +
+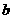 (
(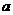 >0)等) .
>0)等) .
56、对于在区间[m,n]上有意义的两个函数f (x)与g (x),如果对任意x∈[m,n]均有| f
(x) – g (x) |≤1,则称f (x)与g (x)在[m,n]上是接近的,否则称f (x)与g (x)在[m,n]上是非接近的,现有两个函数f 1(x)
= loga(x – 3a)与f 2 (x)
= loga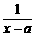 (a > 0,a≠1),给定区间[a
+ 2,a + 3].
(a > 0,a≠1),给定区间[a
+ 2,a + 3].
(1)若f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上都有意义,求a的取值范围;
(2)讨论f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上是否是接近的?
解:(1)要使f 1 (x)与f 2 (x)有意义,则有
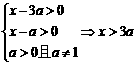
要使f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上有意义,
等价于真数的最小值大于0
即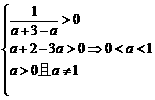
(2)f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上是接近的
 | f 1 (x) – f 2 (x)|≤1
| f 1 (x) – f 2 (x)|≤1

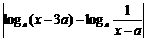 ≤1
≤1
 |loga[(x – 3a)(x – a)]|≤1
|loga[(x – 3a)(x – a)]|≤1
 a≤(x – 2a)2
– a2≤
a≤(x – 2a)2
– a2≤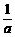
对于任意x∈[a + 2,a + 3]恒成立
设h(x) = (x – 2a)2 – a2,x∈[a + 2,a + 3]
 且其对称轴x = 2a
< 2在区间[a + 2,a + 3]的左边
且其对称轴x = 2a
< 2在区间[a + 2,a + 3]的左边
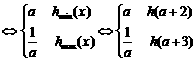
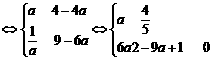

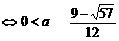
当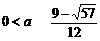 时
时
f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上是接近的
当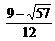 < a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的.
< a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的.
55、对数列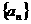 ,规定
,规定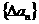 为数列
为数列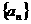 的一阶差分数列,其中
的一阶差分数列,其中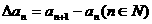 。
。
对自然数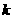 ,规定
,规定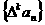 为
为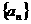 的
的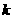 阶差分数列,其中
阶差分数列,其中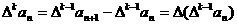 。
。
(1)已知数列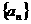 的通项公式
的通项公式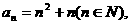 ,试判断
,试判断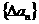 ,
,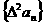 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列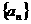 首项
首项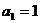 ,且满足
,且满足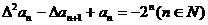 ,求数列
,求数列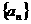 的通项公式。
的通项公式。
(3)对(2)中数列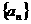 ,是否存在等差数列
,是否存在等差数列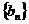 ,使得
,使得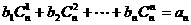 对一切自然
对一切自然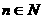 都成立?若存在,求数列
都成立?若存在,求数列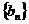 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
解:(1)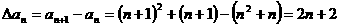 ,∴
,∴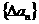 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
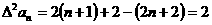
∴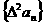 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)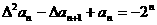 ,即
,即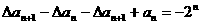 ,即
,即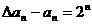 ,∴
,∴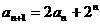
∵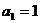 ,∴
,∴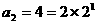 ,
,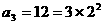 ,
,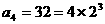 ,猜想:
,猜想: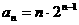
证明:ⅰ)当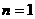 时,
时,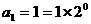 ;
;
ⅱ)假设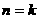 时,
时,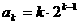
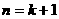 时,
时,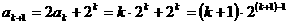 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,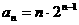
(3)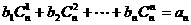 ,即
,即 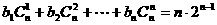
∵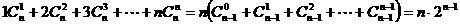
∴存在等差数列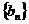 ,
,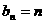 ,使得
,使得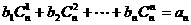 对一切自然
对一切自然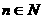 都成立。
都成立。
54、如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数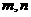 时,输出结果记为
时,输出结果记为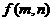 ,且计算装置运算原理如下:
,且计算装置运算原理如下:
①
若Ⅰ、Ⅱ分别输入1,则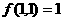 ;②若Ⅰ输入固定的正整数,
;②若Ⅰ输入固定的正整数,
Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,
Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:
(1)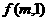 的表达式
的表达式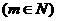 ;(2)
;(2)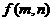 的表达式
的表达式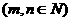 ;
;
(3)若Ⅰ、Ⅱ都输入正整数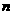 ,则输出结果
,则输出结果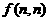 能否为2005?
能否为2005?
若能,求出相应的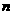 ;若不能,则请说明理由。
;若不能,则请说明理由。
解:(1)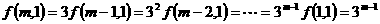
(2)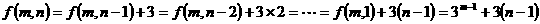
(3)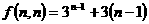 ,∵
,∵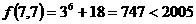 ,
,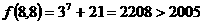
∴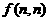 输出结果不可能为
输出结果不可能为 。
。
53、已知函数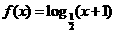 ,当点
,当点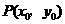 在
在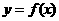 的图像上移动时,
的图像上移动时,
点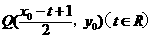 在函数
在函数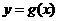 的图像上移动.
的图像上移动.
(1) 若点P坐标为(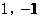 ),点Q也在
),点Q也在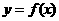 的图像上,求
的图像上,求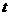 的值;
的值;
(2) 求函数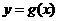 的解析式;
的解析式;
(3) 当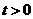 时,试探求一个函数
时,试探求一个函数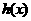 使得
使得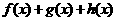 在限定定义域为
在限定定义域为
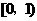 时有最小值而没有最大值.
时有最小值而没有最大值.
解:(1)当点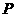 坐标为(
坐标为(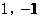 ),点
),点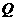 的坐标为
的坐标为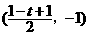 ,…………2分
∵点
,…………2分
∵点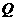 也在
也在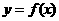 的图像上,∴
的图像上,∴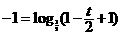 ,即
,即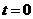 .……5分
.……5分
(根据函数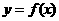 的单调性求得
的单调性求得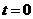 ,请相应给分)
(2)设
,请相应给分)
(2)设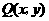 在
在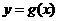 的图像上
则
的图像上
则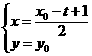 ,即
,即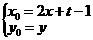 ……………………………………8分
而
……………………………………8分
而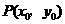 在
在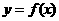 的图像上,∴
的图像上,∴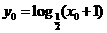 代入得,
代入得,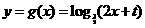 为所求.…………………………………11分
为所求.…………………………………11分
(3)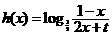 ;或
;或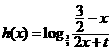 等. …………………15分
如:当
等. …………………15分
如:当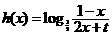 时,
时,
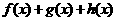
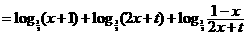
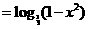
∵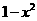 在
在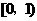 单调递减, ∴
单调递减, ∴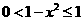 故
故 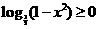 ,
即
,
即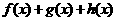 有最小值
有最小值 ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)
(参考思路)在探求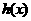 时,要考虑以下因素:①
时,要考虑以下因素:①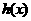 在
在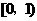 上必须有意义(否则不能参加与
上必须有意义(否则不能参加与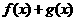 的和运算);②由于
的和运算);②由于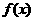 和
和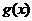 都是以
都是以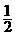 为底的对数,所以构造的函数
为底的对数,所以构造的函数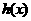 可以是以
可以是以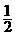 为底的对数,这样与
为底的对数,这样与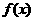 和
和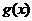 进行的运算转化为真数的乘积运算;③以
进行的运算转化为真数的乘积运算;③以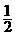 为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去
为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去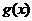 ;⑤乘积的结果可以是
;⑤乘积的结果可以是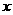 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线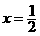 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与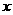 轴已有了一个公共点
轴已有了一个公共点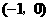 ,故对称轴又应该是
,故对称轴又应该是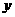 轴或在
轴或在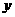 轴的右侧(否则该二次函数的值在
轴的右侧(否则该二次函数的值在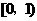 上的值不能恒为正数),即若抛物线与
上的值不能恒为正数),即若抛物线与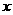 轴的另一个公共点是
轴的另一个公共点是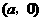 ,则
,则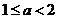 ,且抛物线开口向下.
,且抛物线开口向下.
52、如果一个数列的各项都是实数,且从第二项开始,每一项与它前一项的平方差是相同的常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(1)设数列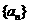 是公方差为
是公方差为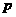 的等方差数列,求
的等方差数列,求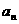 和
和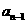
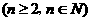 的关系式;
(2)若数列
的关系式;
(2)若数列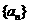 既是等方差数列,又是等差数列,证明该数列为常数列;
(3) 设数列
既是等方差数列,又是等差数列,证明该数列为常数列;
(3) 设数列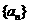 是首项为
是首项为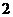 ,公方差为
,公方差为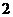 的等方差数列,若将
的等方差数列,若将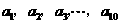 这种顺
这种顺
序的排列作为某种密码,求这种密码的个数.
(1)解:由等方差数列的定义可知: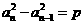
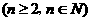 ………………5分
………………5分
(2)证法一:∵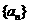 是等差数列,设公差为
是等差数列,设公差为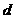 ,则
,则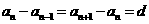 又
又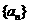 是等方差数列,∴
是等方差数列,∴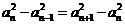 ………………………………7分
∴
………………………………7分
∴ 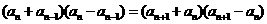 即
即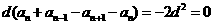 , …………………………………10分
∴
, …………………………………10分
∴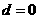 ,即
,即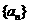 是常数列.…………………………………………………11分
证法二:∵
是常数列.…………………………………………………11分
证法二:∵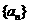 是等差数列,设公差为
是等差数列,设公差为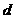 ,则
,则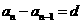 ……1
又
……1
又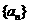 是等方差数列,设公方差为
是等方差数列,设公方差为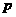 ,则
,则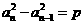 ……2…………7分
1代入2得,
……2…………7分
1代入2得,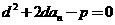 ……3
同理有,
……3
同理有,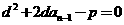 ……4
两式相减得:即
……4
两式相减得:即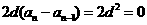 ,…………………………………10分
∴
,…………………………………10分
∴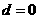 ,即
,即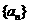 是常数列.………………………………………………11分
是常数列.………………………………………………11分
证法三:(接证法二1、2)
由1、2得出:若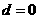 ,则
,则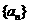 是常数列 …………………8分
是常数列 …………………8分
若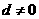 , 则
, 则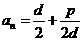 是常数,
∴
是常数,
∴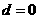 ,矛盾…………10分
,矛盾…………10分
∴ 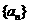 是常数列.
…………………11分
(3)依题意,
是常数列.
…………………11分
(3)依题意, 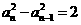
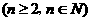 ,
,
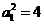 ,
,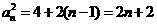 ∴
∴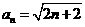 ,或
,或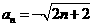 ,
……………………………13分
即该密码的第一个数确定的方法数是
,
……………………………13分
即该密码的第一个数确定的方法数是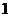 ,其余每个数都有“正”或“负”两种
,其余每个数都有“正”或“负”两种
确定方法,当每个数确定下来时,密码就确定了,即确定密码的方法数是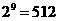 种,
故,这种密码共
种,
故,这种密码共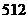 种.…………………………………………………16分
种.…………………………………………………16分
51、已知命题:平面上一矩形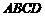 的对角线
的对角线 与边
与边 和
和
所成角分别为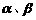 ,则
,则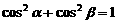 。若把它推广到空
。若把它推广到空
间长方体中,试写出相应的命题形式:____________________
_____________________________________________________。
长方体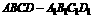 中,对角线
中,对角线 与棱
与棱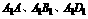 所成的角分别为
所成的角分别为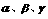 ,则
,则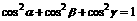 ,
,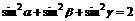 。或是:长方体
。或是:长方体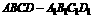 中,对角线
中,对角线 与平面
与平面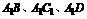 所成的角分别为
所成的角分别为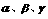 ,则
,则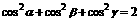 ,
,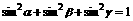 。或是:长方体
。或是:长方体 中,对角面
中,对角面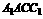 与平面
与平面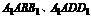 所成的二面角分别为
所成的二面角分别为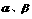 ,则
,则 。
。
50、定义一种运算“*”,对于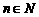 ,满足以下运算性质:
,满足以下运算性质:
① 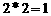 ;②
;② 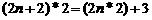 。则
。则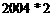 的数值为_____3004_____。
的数值为_____3004_____。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com