
题目列表(包括答案和解析)
16.(本小题满分13分)
解:(1)∵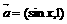 ,
,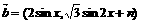
∴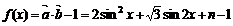
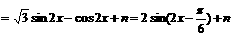
∴函数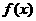 的最小正周期为
的最小正周期为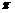
为使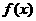 单调递减,则
单调递减,则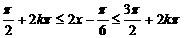
即 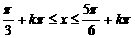
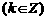
∴函数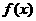 的单调递减区间是
的单调递减区间是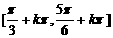
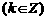
(2)∵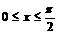 ,∴
,∴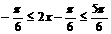
∴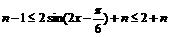
为使用不等式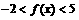 对于
对于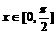 恒成立,则
恒成立,则
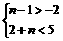 ,即
,即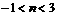
∴实数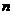 的取值范围是
的取值范围是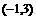
11.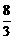 12.8 13.31 14.
12.8 13.31 14.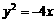 15.⑴ ⑶ ⑷
15.⑴ ⑶ ⑷
1.B 2.B 3.C 4.D 5.C 6.D 7.B 8.C 9.B 10.A
第Ⅱ卷(非选择题 共100分)
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知四边形OABC的各顶点为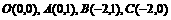 ,矩阵M对应的变换将四边OABC变为四边形
,矩阵M对应的变换将四边OABC变为四边形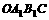 ,且将点A、B分别变为点
,且将点A、B分别变为点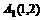 和
和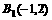 。
。
(I)求矩阵M;
(II)求矩阵M的特征值。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
以极点为原点,极轴为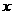 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单
位.圆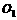 的极坐标方程为
的极坐标方程为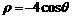 ,圆
,圆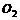 的参数方程为
的参数方程为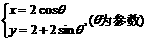 ,求圆
,求圆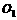 与圆
与圆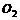 公共弦的长度.
公共弦的长度.
(3)(本小题满分7分)选修4-5:不等式选讲
已知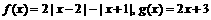 。
。
(I)画出函数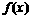 的图象,并根据函数图象写出
的图象,并根据函数图象写出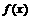 的单调区间;
的单调区间;
 (II)若关于
(II)若关于 的不等式
的不等式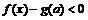 有解,求实数
有解,求实数 的取值范围。
的取值范围。
福州三中高中毕业班适应性测试答案
数学(理科)试卷
第I卷(选择题 共50分)
20.(本小题满分14分)
设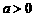 ,函数
,函数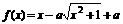 。
。
(1)若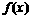 在区间
在区间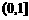 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(2)求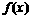 在区间
在区间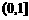 上的最大值;
上的最大值;
(3)数列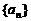 满足
满足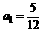 ,
,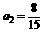 ,
,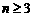 时
时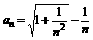 。数列
。数列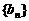 满足
满足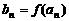 ,
,
若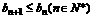 恒成立,试求实数
恒成立,试求实数 的最小值。
的最小值。
19.(本小题满分13分)
已知椭圆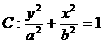 的一个焦点的坐标是
的一个焦点的坐标是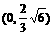 且率心率
且率心率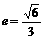
(1)求椭圆 的方程;
的方程;
(2)设圆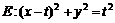
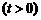 ,是否存在实数
,是否存在实数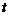 使圆
使圆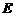 与椭圆
与椭圆 交于
交于 、
、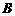 两点,且
两点,且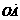 ·
·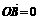 。若存在,请求出实数
。若存在,请求出实数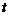 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)在(2)的条件,设 、
、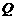 是圆
是圆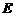 上的两动点,满足
上的两动点,满足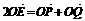 (
(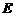 是圆
是圆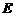 的圆心),点
的圆心),点 是椭圆
是椭圆 上的动点,试求
上的动点,试求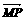 ·
·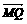 的最大值。
的最大值。
18.(本小题满分13分)
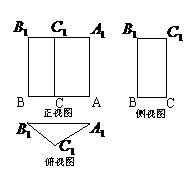
三棱柱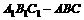 中,D为底边AB的中点,
中,D为底边AB的中点,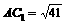 ,其三视图如图所示,其中正视图
,其三视图如图所示,其中正视图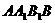 和侧视图
和侧视图 都是矩形,俯视图
都是矩形,俯视图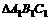 中,
中,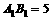 ,
,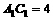 ,
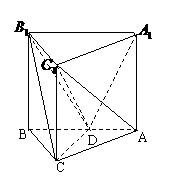
,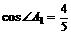 。在三棱柱
。在三棱柱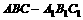 中
中
 (1)求证:
(1)求证: ;
;
(2)求点A到平面 的距离;
的距离;
(3)求锐二面角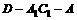 的余弦值。
的余弦值。
17.(本小题满分13分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成500
万元的损失。现有甲、乙两种相互独立的预防措施可供采用,单独采用甲、乙预防措施所
需费用分别60万元和42万元,采用相应预防措施后此突发事件不发生的概率分别是0.9
和0.85。若预防方案允许单独采用、联合采用或不采用,请确定预防方案使总费用最少。
(总费用=采取预防措施费用+发生突发事件损失的期望值)
16.(本小题满分13分)
已知函数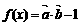 ,其中
,其中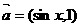 ,
,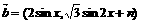 。
。
(1)求函数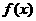 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)当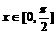 ,不等式
,不等式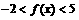 恒成立,求实数
恒成立,求实数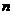 的取值范围。
的取值范围。
15.定义:设常数M对于一切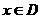 ,
,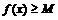 恒成立(D为
恒成立(D为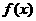 的定义域),若这样的M有最大值
的定义域),若这样的M有最大值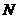 ,则称N为函数
,则称N为函数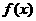 的下确界。下列有四个函数:
的下确界。下列有四个函数:
⑴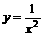 ;⑵
;⑵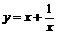 ;⑶
;⑶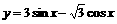 ;⑷
;⑷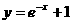
则其中具有下确界的函数是________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com