
题目列表(包括答案和解析)
18.(16分)求关于x的方程ax2-(a2+a+1)x+a+1=0至少有一个正根的充要条件.
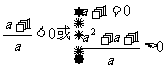
解 方法一 若a=0,则方程变为-x+1=0,x=1满足条件,若a≠0,则方程至少有一个正根等价于
 ?
?
或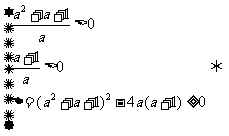 -1<a<0或a>0.
-1<a<0或a>0.
综上:方程至少有一正根的充要条件是a>-1.
方法二 若a=0,则方程即为-x+1=0,
∴x=1满足条件;若a≠0,∵Δ=(a2+a+1)2-4a(a+1)=(a2+a)2+2(a2+a)+1-4a(a+1)
=(a2+a)2-2a(a+1)+1=(a2+a-1)2≥0,∴方程一定有两个实根.
故而当方程没有正根时,应有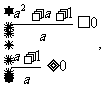 解得a≤-1,
解得a≤-1,
∴至少有一正根时应满足a>-1且a≠0,
综上:方程有一正根的充要条件是a>-1.
17.(14分)已知p:|1-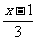 |≤2,q:x2-2x+1-m2≤0(m>0),且
|≤2,q:x2-2x+1-m2≤0(m>0),且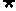 p是
p是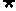 q的必要而不充分条件,求实数m的取值范围.
q的必要而不充分条件,求实数m的取值范围.
解 方法一 由x2-2x+1-m2≤0,得1-m≤x≤1+m,
∴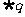 :A={x|x>1+m或x<1-m,m>0},由|1-
:A={x|x>1+m或x<1-m,m>0},由|1-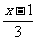 |≤2,得-2≤x≤10,
|≤2,得-2≤x≤10,
∴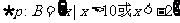 ,∵
,∵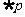 是
是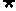 q的必要而不充分条件,
q的必要而不充分条件,
∴A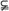 B
B 解得m≥9.
解得m≥9.
方法二 ∵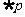 是
是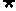 q的必要而不充分条件,
q的必要而不充分条件,
∴q是p的必要而不充分条件,∴p是q的充分而不必要条件,
由x2-2x+1-m2≤0.得1-m≤x≤1+m(m>0),∴q:B=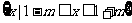 .
.
又由|1-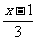 |≤2,得-2≤x≤10,∴p:A=
|≤2,得-2≤x≤10,∴p:A=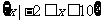 .又∵p是q的充分而不必要条件.
.又∵p是q的充分而不必要条件.
∴B A
A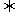
 ,解得m≥9.
,解得m≥9.
16.(14分)已知集合U=R, UA=
UA=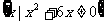 ,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
解 ∵A={0,-6},A∪B=A,∴B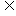 A.
A.
(1)当B=A时,由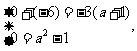 得a=1,
得a=1,
(2)当B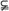 A时,
A时,
①若B=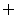 ,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-
,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-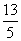 <a<-1.
<a<-1.
②若B≠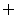 ,则方程x2+3(a+1)x+a2-1=0有相等的实根,
,则方程x2+3(a+1)x+a2-1=0有相等的实根,
即Δ=0,即a=-1或a=-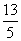 .由a=-1得B={0},有B
.由a=-1得B={0},有B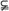 A;
A;
由a=-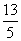 ,得B={
,得B={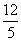 }不满足B
}不满足B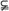 A,舍去,综上可知,-
A,舍去,综上可知,-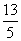 <a≤-1或a=1.
<a≤-1或a=1.
15.(14分)设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若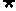 p是
p是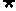 q的必要不充分条件,求实数a的取值范围.
q的必要不充分条件,求实数a的取值范围.
解 设A={x|(4x-3)2≤1},B={x|x2-(2a+1)x+a(a+1)≤0},易知A={x|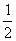 ≤x≤1},B={x|a≤x≤a+1}.
≤x≤1},B={x|a≤x≤a+1}.
由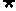 p是
p是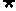 q的必要不充分条件,从而p是q的充分不必要条件,即A
q的必要不充分条件,从而p是q的充分不必要条件,即A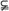 B,∴
B,∴
故所求实数a的取值范围是[0,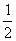 ].
].
14.下列命题中:
①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为: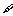 x∈R,x2+2x+2≤0,则
x∈R,x2+2x+2≤0,则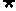 p为:
p为: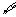 x∈R,x2+2x+2>0;
x∈R,x2+2x+2>0;
③若椭圆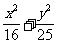 =1的两焦点为F1、F2,且弦AB过F1点,则△ABF2的周长为16;
=1的两焦点为F1、F2,且弦AB过F1点,则△ABF2的周长为16;
④若a<0,-1<b<0,则ab>ab2>a.
所有正确命题的序号是 .
答案 ②④
13.不等式|x|<a的一个充分条件为0<x<1,则a的取值范围为 .
答案 a≥1
12.已知条件p:|x+1|>2,条件q:5x-6>x2,则非p是非q的 条件.
答案 充分不必要
11.设集合A={5,log2(a+3)},集合B={a,b},若A∩B={2},则A∪B= .
答案 {1,2,5}
10.(2008·浙江理,2)已知U=R,A={x|x>0},B={x|x≤-1},则(A∩ UB)∪(B
UB)∪(B
 UA)= .
UA)= .
答案 {x|x>0或x≤-1}
9.若数列{an}满足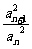 =p(p为正常数,n∈N*),则称{an}为“等方比数列”.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.
甲:数列{an}是等方比数列;
乙:数列{an}是等比数列,则甲是乙的 条件.
答案 必要不充分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com