
题目列表(包括答案和解析)
下列命题正确的是 ( )
A.函数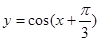 的图像是关于点
的图像是关于点 成中心对称的图形
成中心对称的图形
B.函数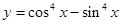 的最小正周期为2
的最小正周期为2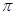
C.函数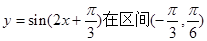 内单调递增
内单调递增
D.函数 的图像是关于直线
的图像是关于直线 成轴对称的图形
成轴对称的图形
下列命题正确的是( )
A.函数 的图像是关于点
的图像是关于点 成中心对称的图形
成中心对称的图形
B.函数 的最小正周期为2
的最小正周期为2
C.函数 内单调递增
内单调递增
D.函数 的图像是关于直线
的图像是关于直线 成轴对称的图形
成轴对称的图形
下列命题正确的是 ( )
A.函数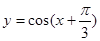 的图像是关于点 的图像是关于点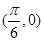 成中心对称的图形 成中心对称的图形 |
B.函数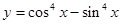 的最小正周期为2 的最小正周期为2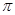 |
C.函数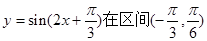 内单调递增 内单调递增 |
D.函数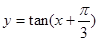 的图像是关于直线 的图像是关于直线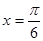 成轴对称的图形 成轴对称的图形 |
若函数 的图像关于点
的图像关于点 成中心对称,则函数
成中心对称,则函数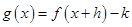 一定是( )
一定是( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.既不是奇函数也不是偶函数
若函数 的图像关于点
的图像关于点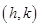 成中心对称,则函数
成中心对称,则函数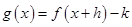 一定是( )
一定是( )
| A.奇函数 |
| B.偶函数 |
| C.既是奇函数又是偶函数 |
| D.既不是奇函数也不是偶函数 |
CACD CCBA
9、.files/image098.gif) 10、2:1 11、
10、2:1 11、.files/image100.gif) 12、
12、.files/image102.gif) 13、4
13、4
14、a<-1 15、.files/image104.gif)
16、
.files/image106.gif) 17、解:(I)依题意
17、解:(I)依题意.files/image108.gif)
.files/image110.gif) …………2分
…………2分
.files/image112.gif)
.files/image114.gif) …………4分
…………4分
.files/image116.gif) bn=8+8×(n-1)=8n …………5分
bn=8+8×(n-1)=8n …………5分
(II).files/image118.gif) …………6分
…………6分
.files/image120.gif)
.files/image122.gif) …………12分
…………12分
18、(1)3.files/image124.gif)
(2)底面边长为2,高为4是,体积最大,最大体积为16
19、
略解、(1)因为f′(x)=3ax2+2x-1,依题意存在(2,+∞)的非空子区间使3ax2+2x-1>0成立,即.files/image126.gif) 在x∈(2,+∞)某子区间上恒成立,令h(x)=
在x∈(2,+∞)某子区间上恒成立,令h(x)=.files/image128.gif) ,求得h(x)的最小值为
,求得h(x)的最小值为.files/image130.gif) ,故
,故.files/image132.gif)
(2)由已知a>0
令f′(x)=3ax2+2x-1>0
得.files/image134.gif) 故f(x)在区间(
故f(x)在区间(.files/image068.gif) )上是减函数,
)上是减函数,.files/image136.gif) 即f(x)在区间(
即f(x)在区间(.files/image068.gif) )上恒大于零。故当a>0时,函数在f(x)在区间(
)上恒大于零。故当a>0时,函数在f(x)在区间(.files/image068.gif) )上不存在零点
)上不存在零点
20、(1)f(1)=3………………………………………………………………………………(1分)
f(2)=6………………………………………………………………………………(2分)
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n…………………………………………………………………………(4分)
(2).files/image138.gif) ………………………………………………(9分)
………………………………………………(9分)
.files/image140.gif)
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=.files/image142.gif)
∴m≥.files/image142.gif) ………………………………………………………………()
………………………………………………………………()
.files/image144.gif)
21、解:(Ⅰ)设.files/image146.gif) ,
,
.files/image148.gif)
.files/image150.gif)
.files/image152.gif) 且
且.files/image154.gif) , …………………2分
, …………………2分
.files/image156.gif) …………………3分
…………………3分
.files/image158.gif) .
………………………………………………4分
.
………………………………………………4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点).
…………………………………………5分
(Ⅱ)解法一:(1)当直线.files/image088.gif) 垂直于
垂直于.files/image078.gif) 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有.files/image090.gif) ;
;
……………6分
.files/image162.gif) (2)当直线
(2)当直线.files/image088.gif) 与
与.files/image078.gif) 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线.files/image088.gif) 的方程为
的方程为.files/image164.gif) ,
,.files/image166.gif) ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
.files/image168.gif)
消去.files/image078.gif) 并整理,得
并整理,得
.files/image171.gif) ,
,
.files/image173.gif) . ……………7分
. ……………7分
设直线AE和BE的斜率分别为.files/image175.gif) ,则:
,则:
.files/image177.gif) =
=.files/image179.gif)
.files/image181.gif)
.files/image183.gif)
.files/image185.gif)
.files/image187.gif) . …………………9分
. …………………9分
.files/image189.gif) ,
,
.files/image191.gif) ,
,
.files/image193.gif) ,
,.files/image195.gif)
.files/image197.gif) .
.
综合(1)、(2)可知.files/image090.gif) .
…………………10分
.
…………………10分
.files/image198.gif) 解法二:依题意,设直线
解法二:依题意,设直线.files/image088.gif) 的方程为
的方程为.files/image200.gif) ,
,.files/image166.gif) ,则A,B两点的坐标满足方程组:
,则A,B两点的坐标满足方程组:
.files/image202.gif)
消去.files/image078.gif) 并整理,得
并整理,得
.files/image204.gif) ,
,
.files/image206.gif) . ……………7分
. ……………7分
设直线AE和BE的斜率分别为.files/image175.gif) ,则:
,则:
.files/image177.gif) =
=.files/image179.gif)
.files/image181.gif)
.files/image183.gif)
.files/image185.gif)
.files/image208.gif) . …………………9分
. …………………9分
.files/image189.gif) ,
,
.files/image191.gif) ,
,
.files/image193.gif) ,
,.files/image195.gif)
.files/image197.gif) . ……………………………………………………10分
. ……………………………………………………10分
(Ⅲ)假设存在满足条件的直线.files/image210.gif) ,其方程为
,其方程为.files/image212.gif) ,AD的中点为
,AD的中点为.files/image214.gif) ,
,.files/image210.gif) 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则.files/image216.gif) ,
,.files/image214.gif) 点的坐标为
点的坐标为.files/image218.gif) .
.
.files/image220.gif)
.files/image222.gif) ,
,
.files/image224.gif) ,
,
.files/image226.gif)
.files/image228.gif)
.files/image230.gif) .
…………………………12分
.
…………………………12分
.files/image232.gif) ,
,
令.files/image234.gif) ,得
,得.files/image236.gif)
此时,.files/image238.gif) .
.
∴当.files/image240.gif) ,即
,即.files/image242.gif) 时,
时,.files/image244.gif) (定值).
(定值).
∴当.files/image242.gif) 时,满足条件的直线
时,满足条件的直线.files/image210.gif) 存在,其方程为
存在,其方程为.files/image246.gif) ;当
;当.files/image248.gif) 时,满足条件的直线
时,满足条件的直线.files/image210.gif) 不存在.
不存在.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com