
题目列表(包括答案和解析)
【2012高考江苏26】(10分)设集合![]() ,
,![]() .记
.记![]() 为同时满足下列条件的集合
为同时满足下列条件的集合![]() 的个数:
的个数:
①![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 。
。
(1)求![]() ;
;
(2)求![]() 的解析式(用
的解析式(用![]() 表示).
表示).
某市投资甲、乙两个工厂,2011年两工厂的产量均为100万吨,在今后的若干年内,甲工厂的年产量每年比上一年增加10万吨,乙工厂第 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 年的年产量分别为
年的年产量分别为 万吨和
万吨和 万吨.
万吨.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若某工厂年产量超过另一工厂年产量的2倍,则将另一工厂兼并,问到哪一年底,其中哪一个工厂被另一个工厂兼并.
【解析】本试题主要考查数列的通项公式的运用。
第一问由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二问,考查等差数列与等比数列的综合,考查用数列解决实际问题,其步骤是建立数列模型,进行计算得出结果,再反馈到实际中去解决问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.
解:(Ⅰ)由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的产量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工厂将被乙工厂兼并
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(I)从袋中随机抽取一个球,将其编号记为 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为 .求关于
.求关于 的一元二次方程
的一元二次方程 有实根的概率;
有实根的概率;
(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域 内的概率.
内的概率.
【解析】第一问利用古典概型概率求解所有的基本事件数共12种,然后利用方程 有实根,则满足△=4a2-4b2≥0,即a2≥b2。,这样求得事件发生的基本事件数为6种,从而得到概率。第二问中,利用所有的基本事件数为16种。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16种。在求解满足
有实根,则满足△=4a2-4b2≥0,即a2≥b2。,这样求得事件发生的基本事件数为6种,从而得到概率。第二问中,利用所有的基本事件数为16种。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16种。在求解满足 的基本事件数为(1,1) (2,1) (2,2) (3,1) 共4种,结合古典概型求解得到概率。
的基本事件数为(1,1) (2,1) (2,2) (3,1) 共4种,结合古典概型求解得到概率。
(1)基本事件(a,b)有:(1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)共12种。
∵ 有实根, ∴△=4a2-4b2≥0,即a2≥b2。
有实根, ∴△=4a2-4b2≥0,即a2≥b2。
记“ 有实根”为事件A,则A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6种。
有实根”为事件A,则A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6种。
∴PA.=  。 …………………6分
。 …………………6分
(2)基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,4) (4,1) (4,2) (4,3) (4,4)共16种。
记“点P落在区域 内”为事件B,则B包含的事件有:
内”为事件B,则B包含的事件有:
(1,1) (2,1) (2,2) (3,1) 共4种。∴PB.=
某省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻
与时刻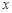 (时) 的关系为
(时) 的关系为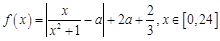 ,其中
,其中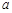 是与气象有关的参数,且
是与气象有关的参数,且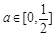 .
.
(1)令 ,
, 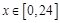 ,写出该函数的单调区间,并选择其中一种情形进行证明;
,写出该函数的单调区间,并选择其中一种情形进行证明;
(2)若用每天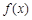 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作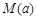 ,求
,求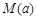 ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
【解析】第一问利用定义法求证单调性,并判定结论。
第二问(2)由函数的单调性知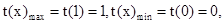 ,
,
∴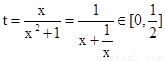 ,即t的取值范围是
,即t的取值范围是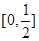 .
.
当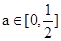 时,记
时,记
则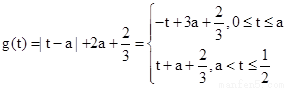
∵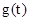 在
在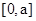 上单调递减,在
上单调递减,在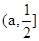 上单调递增,
上单调递增,
第三问因为当且仅当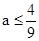 时,
时,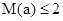 .
.
故当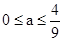 时不超标,当
时不超标,当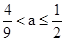 时超标.
时超标.
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到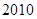 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为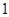 ,
,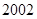 年编号为
年编号为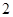 ,…,
,…,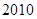 年编号为
年编号为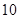 .数据如下:
.数据如下:
|
年份( |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数( |
3 |
5 |
8 |
11 |
13 |
14 |
17 |
22 |
30 |
31 |
(1)从这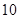 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有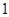 年多于
年多于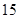 人的概率;
人的概率;
(2)根据前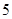 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出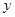 关于
关于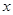 的回归方程
的回归方程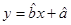 ,并计算第
,并计算第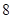 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。
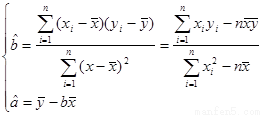
【解析】(1)设考入大学人数至少有1年多于15人的事件为A则P(A)=1-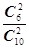 =
=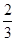 (4’)
(4’)
(2)由已知数据得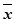 =3,
=3,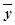 =8,
=8,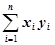 =3+10+24+44+65=146
=3+10+24+44+65=146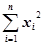 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
则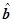 =
=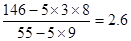 ,
,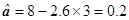 (9’)
(9’)
则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com