
题目列表(包括答案和解析)
已知直线![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到点
上的点到点![]() 的最大距离为8.
的最大距离为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,直线
,直线![]() .试证明当点
.试证明当点![]() 在椭圆
在椭圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 恒相交;并求直线
恒相交;并求直线![]() 被圆
被圆![]() 所截得的弦长的取值范围.
所截得的弦长的取值范围.
已知直线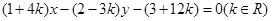 所经过的定点
所经过的定点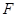 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 上的点到点
上的点到点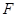 的最大距离为8.则椭圆
的最大距离为8.则椭圆 的标准方程为 .
的标准方程为 .
已知直线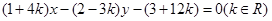 所经过的定点
所经过的定点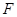 恰好是椭圆
恰好是椭圆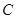 的一个焦点,且椭圆
的一个焦点,且椭圆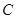 上的点到点
上的点到点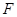 的最大距离为8.则椭圆
的最大距离为8.则椭圆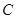 的标准方程为 .
的标准方程为 .
已知直线![]()
![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到点
上的点到点![]() 的最大距离为3.
的最大距离为3.
(Ⅰ) 求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ) 设过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
已知直线![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到
上的点到
点![]() 的最大距离为8.
的最大距离为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,直线
,直线![]() .试证明:当点
.试证明:当点![]() 在椭圆
在椭圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 恒相交,并求直线
恒相交,并求直线![]() 被圆
被圆![]() 所截得弦长
所截得弦长![]() 的取值范围.
的取值范围.
一、选择题:
|