已知直线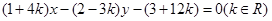
所经过的定点
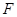恰好是椭圆
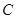的一个焦点,且椭圆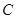上的点到点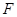的最大距离为8.则椭圆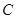的标准方程为 ．
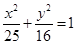
解析试题分析：条件中给出一个直线系，需要先求出直线所过的定点，根据定点是椭圆的焦点，及椭圆C上的点到点F的最大距离为8，写出椭圆中三个字母系数要满足的条件，解方程组得到结果，写出椭圆的方程解：由（1+4k）x-（2-3k）y-（3+12k）=0得（x-2y-3）+k（4x+3y-12）=0，由x-2y-3=0，4x+3y-12=0，解得F（3，0）．设椭圆C的标准方程为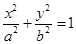
(a＞b＞0)，则，c=3,a+c=8，
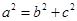，解得解得 a=5，b=4，c=3，从而椭圆C的标准方程为。
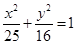考点：椭圆方程的求解
点评：本题考查直线与圆锥曲线之间的关系，题目中首先求椭圆的方程，这是这类题目常用的一种形式，属于基础题．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
得顶点
、
分别是离心率为
的圆锥曲线
的焦点，顶点
在该曲线上，一同学已正确地推得，当
时有
，类似地，当
时，有 .
的准线方程是 ．
与抛物线
有一个公共的焦点，且双曲线上的点到坐标原点的最短距离为1，则该双曲线的标准方程是___________。
的左准线与
轴的交点，点A坐标为(0,b)，若满足
点P在双曲线上，则双曲线的离心率为_____________
的直线
与抛物线
交于
两点，记线段
的中点为
，过点
的直线为
,
，则直线
__ ．
，它的一个焦点是
，则双曲线的标准方程是 .
是双曲线
的两个焦点，P是C上一点，若
且
的最小内角为
，则C的离心率为___。
交抛物线
于
两点.若该抛物线上存在点
，使得
为直角，则
的取值范围为___________.