
题目列表(包括答案和解析)
已知数列 满足:
满足: ,
,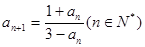
(Ⅰ)计算 的值;
的值;
(Ⅱ)由(Ⅰ)的结果猜想 的通项公式,并用数学归纳法证明你的结论.
的通项公式,并用数学归纳法证明你的结论.
【解析】本试题主要考查了数列的通项公式的求解和猜想和数学归纳法的证明。
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式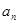 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当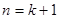 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
天津精通高考复读学校数学教研组组长 么世涛
一、选择题 :1-4, BBBB ;5-8,DABD。
提示:1.
2.
3.用 代替
代替 得
得
4.
5. ,
, 或
或
6.
7.略
8.


二、填空题:9.60; 10. 15:10:20 ; 11. ; 12.
; 12. ;
;
13.0.74 ; 14. ①、 ;②、圆;③.
;②、圆;③.
提示:
9.
10. ,
, ,
,
11. ,
,
12. ,
, ,
, ,
,
 ,
,
13.
14.略
三、解答题
15. 解:(1) .
.
(2)设抽取 件产品作检验,则
件产品作检验,则 ,
,
 ,得:
,得: ,即
,即 
故至少应抽取8件产品才能满足题意.
16. 解:由题意得 ,
, ,原式可化为
,原式可化为 ,
,
而
 ,
,
故原式= .
.
17. 解:(1)显然 ,连接
,连接 ,∵
,∵ ,
, ,
,
∴ .由已知
.由已知 ,∴
,∴ ,
, .
.
∵ ∽
∽ ,
,  ,
,
∴ 即
即  .
.
∴ .
.
(2) 
当且仅当 时,等号成立.此时
时,等号成立.此时 ,即
,即 为
为 的中点.于是由
的中点.于是由 ,知平面
,知平面 ,
, 是其交线,则过
是其交线,则过 作
作
 。
。
∴ 就是
就是 与平面
与平面 所成的角.由已知得
所成的角.由已知得 ,
, ,
,
∴ ,
,  ,
,  .
.
(3) 设三棱锥 的内切球半径为
的内切球半径为 ,则
,则

∵ ,
, ,
, ,
, ,
, ,
,
∴ .
.
18. 解: (1)  ,
,
(2) ∵  ,
,
∴当 时,
时,

∴当 时,
时, ,
,
∵ ,
, ,
, ,
, .
.
∴  的最大值为
的最大值为 或
或 中的最大者.
中的最大者.
∵ 
∴ 当 时,
时, 有最大值为
有最大值为
 .
.
19.(1)解:∵函数 的图象过原点,
的图象过原点,
∴ 即
即 ,
,
∴ .
.
又函数 的图象关于点
的图象关于点 成中心对称,
成中心对称,
∴ ,
, .
.
(2)解:由题意有 即
即 ,
,
即 ,即
,即 .
.
∴数列{ }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴ ,即
,即 . ∴
. ∴ .
.
∴  ,
, ,
, ,
, .
.
(3)证明:当 时,
时,

故 
20. (1)解:∵ ,又
,又 ,
,
∴ .
又∵
.
又∵
 ,且
,且
∴  .
.
(2)解:由 ,
, ,
, 猜想
猜想
(3)证明:用数学归纳法证明:
①当 时,
时, ,猜想正确;
,猜想正确;
②假设 时,猜想正确,即
时,猜想正确,即
1°若 为正奇数,则
为正奇数,则 为正偶数,
为正偶数, 为正整数,
为正整数,

2°若 为正偶数,则
为正偶数,则 为正整数,
为正整数,
 ,又
,又 ,且
,且
所以
即当 时,猜想也正确
时,猜想也正确
由①,②可知, 成立.
成立.
(二)
一、1-4,AABB,5-8,CDCB;
提示: 1.  即
即 

2.  即
即 
3.  即
即 ,也就是
,也就是  ,
,
4.先确定是哪两个人的编号与座位号一致,有 种情况,如编号为1的人坐1号座位,且编号为2的人坐2号座位有以下情形:
种情况,如编号为1的人坐1号座位,且编号为2的人坐2号座位有以下情形:
|