
题目列表(包括答案和解析)
(12分)已知函数![]() 在
在![]() 处取得极值2.
处取得极值2.
(1)求函数![]() 的表达式;
的表达式;
(2)当![]() 满足什么条件时,函数
满足什么条件时,函数![]() 在区间
在区间![]() 上单调递增?
上单调递增?
(本题12分)某地区上年度电价为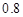 元/kW•h,年用电量为
元/kW•h,年用电量为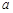 kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为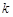 ),该地区电力的成本价为0.30元/ kW•h.
),该地区电力的成本价为0.30元/ kW•h.
(1)写出本年度电价下调后,电力部门的收益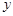 与实际电价
与实际电价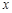 之间的函数关系式;
之间的函数关系式;
(2)设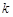 =
=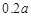 ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价 本价))
本价))
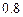 元/kW•h,年用电量为
元/kW•h,年用电量为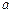 kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为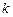 ),该地区电力的成本价为0.30元/ kW•h.
),该地区电力的成本价为0.30元/ kW•h.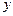 与实际电价
与实际电价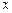 之间的函数关系式;
之间的函数关系式;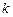 =
=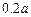 ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价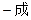 本价))
本价))(本小题满分12分)(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒。当你到达路口时,求不是红灯的概率。(2)已知关于x的一元二次函数![]() 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率。
上是增函数的概率。
(本小题满分12分)
(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒。当你到达路口时,求不是红灯的概率。
(2)已知关于x的一元二次函数![]() 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率。
上是增函数的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com