
题目列表(包括答案和解析)
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
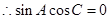

又由 得
得 即
即

又由 得
得 即
即

又
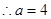 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

函数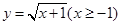 的反函数为
的反函数为
(A)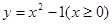 (B)
(B)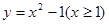
(C)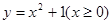 (D)
(D)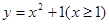
【解析】 因为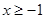 所以
所以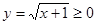 .由
.由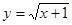 得,
得,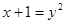 ,所以
,所以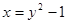 ,所以反函数为
,所以反函数为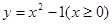 ,选A.
,选A.
如图,在直三棱柱 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形, ,
, 为棱
为棱 上一点,且平面
上一点,且平面 平面
平面 .
.
(Ⅰ)求证: 点为棱
点为棱 的中点;
的中点;
(Ⅱ)判断四棱锥 和
和 的体积是否相等,并证明。
的体积是否相等,并证明。

【解析】本试题主要考查了立体几何中的体积问题的运用。第一问中,
易知 ,
, 面
面 。由此知:
。由此知: 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
的中点.
(2)中由A1B1⊥平面B1C1CD,BC⊥平面A1ABD,D为BB1中点,可以得证。
(1)过点 作
作 于
于 点,取
点,取 的中点
的中点 ,连
,连 。
。 面
面 面
面 且相交于
且相交于 ,面
,面 内的直线
内的直线 ,
, 面
面 。……3分
。……3分
又 面
面 面
面 且相交于
且相交于 ,且
,且 为等腰三角形,易知
为等腰三角形,易知 ,
, 面
面 。由此知:
。由此知: ,从而有
,从而有 共面,又易知
共面,又易知 面
面 ,故有
,故有 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
…6分
的中点.
…6分
(2)相等.ABC-A1B1C1为直三棱柱,∴BB1⊥A1B1,BB1⊥BC,又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)∴VA1-B1C1CD=1 /3 SB1C1CD•A1B1=1/ 3 ×1 2 (B1D+CC1)×B1C1×A1B1VC-A1ABD=1 /3 SA1ABD•BC=1 /3 ×1 2 (BD+AA1)×AB×BC∵D为BB1中点,∴VA1-B1C1CD=VC-A1ABD
在△ABC中,角A、B、C的对边分别为a、b、c,向量 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
=
(Ⅰ)求角B的大小;
(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
【解析】本试题主要考查了向量的数量积和三角函数,以及解三角形的综合运用
第一问中由条件|p +q |=| p -q |,两边平方得p·q=0,又
p=(sinA,b+c),q=(a-c,sinC-sinB),代入得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,
即 ,又由余弦定理
,又由余弦定理 =2acosB,所以cosB=
=2acosB,所以cosB= ,B=
,B=
第二问中,m=(sin(C+ ),
), ),n=(2k,cos2A) (k>1),m·n=2ksin(C+
),n=(2k,cos2A) (k>1),m·n=2ksin(C+ )+
)+ cos2A=2ksin(C+B) +
cos2A=2ksin(C+B) + cos2A
cos2A
=2ksinA+ -
- =-
=- +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).
(k>1).
而0<A< ,sinA∈(0,1],故当sin=1时,m·n取最大值为2k-
,sinA∈(0,1],故当sin=1时,m·n取最大值为2k- =3,得k=
=3,得k= .
.
在 中,
中, 是三角形的三内角,
是三角形的三内角, 是三内角对应的三边,已知
是三内角对应的三边,已知 成等差数列,
成等差数列, 成等比数列
成等比数列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一问中利用依题意 且
且 ,故
,故
第二问中,由题意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,从而得到结论。
,从而得到结论。
(1)依题意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由题意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入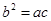 得
得

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com