
题目列表(包括答案和解析)
函数![]() 的定义域为R,且
的定义域为R,且![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() 上的最小值为
上的最小值为![]() ,试求f(x)的解析式;
,试求f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下记![]() 试比较
试比较![]() 与
与
![]() 的大小并证明你的结论.
的大小并证明你的结论.
函数![]() 的定义域为
的定义域为![]() ,并满足条件
,并满足条件
① 对任意![]() ,有
,有![]() ;
;
② 对任意![]() ,有
,有![]() ;
;
③ ![]() .
.
(1)求![]() 的值;
的值;
![]() (2)求证:
(2)求证:![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(3)若![]() ,且
,且![]() ,求证
,求证![]() .
.
函数![]() 的定义域为(0,1](
的定义域为(0,1](![]() 为实数).
为实数).
⑴当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
⑵若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
⑶求函数![]() 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时![]() 的值
的值
函数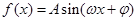 的图像如图所示,其中
的图像如图所示,其中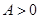 ,
,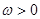 ,
,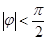 .
.
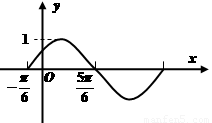
(1)求出A、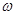 、
、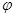 的值;
的值;
(2)由函数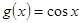 经过平移变换可否得到函数
经过平移变换可否得到函数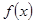 的图像?若能,平移的最短距离是多少个单位?否则,说明理由.
的图像?若能,平移的最短距离是多少个单位?否则,说明理由.
函数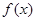 的定义域为
的定义域为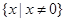 ,且满足对于定义域内任意的
,且满足对于定义域内任意的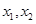 都有等式
都有等式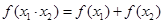 .
.
(1)求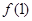 的值;
的值;
(2)判断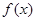 的奇偶性并证明;
的奇偶性并证明;
(3)若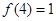 ,且
,且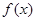 在
在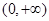 上是增函数,解关于
上是增函数,解关于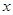 的不等式
的不等式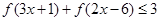 .
.
一、选择题:(每小题5分,共60分)
ADBBC CDCDC BD
二、填空题:(每小题4分,共16分)
13. 试题.files/image176.gif)
试题.files/image178.gif)
试题.files/image180.gif) .
.
14、33
15、试题.files/image182.gif)
16. ① ③ ⑤
三、解答题
17、【解】由题意,得试题.files/image184.gif)
试题.files/image186.gif)
试题.files/image188.gif) .……4分
.……4分
(1)∵试题.files/image110.gif) ,
,试题.files/image114.gif) ,∴
,∴试题.files/image191.gif) ,
,
∴试题.files/image193.gif) . ……8分
. ……8分
(2)由图象变换得,平移后的函数为试题.files/image195.gif) ,而平移后的图象关于原点对称.
,而平移后的图象关于原点对称.
∴试题.files/image197.gif) 且
且试题.files/image199.gif) ,即
,即试题.files/image201.gif) 且
且试题.files/image203.gif) ,
,
∵试题.files/image205.gif) ,∴
,∴试题.files/image207.gif) ,即
,即试题.files/image209.gif) .……12分
.……12分
18、【解】解法一(I)证明:
连接A1B,设A1B∩AB1 = E,连接DE.
∵ABC―A1B
∴四边形A1ABB1是正方形,
∴E是A1B的中点,
又D是BC的中点,
∴DE∥A
∵DE试题.files/image211.gif) 平面AB1D,A
平面AB1D,A试题.files/image213.gif) 平面AB1D,
平面AB1D,
∴A
(II)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.
∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1,
∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1
∴∠FGD是二面角B―AB1―D的平面角 …………………………6分
设A试题.files/image215.gif)
在△ABE中,试题.files/image217.gif) ,
,
在Rt△DFG中,试题.files/image219.gif) ,
,
所以,二面角B―AB1―D的大小为试题.files/image221.gif) …………………………8分
…………………………8分
(III)解:∵平面B1BCC1⊥平面ABC,且AD⊥BC,
∴AD⊥平面B1BCC1,又AD试题.files/image211.gif) 平面AB1D,∴平面B1BCC1⊥平面AB1D.
平面AB1D,∴平面B1BCC1⊥平面AB1D.
在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H,
则CH的长度就是点C到平面AB1D的距离. ……………………………10分
由△CDH∽△B1DB,得试题.files/image224.gif)
|