
题目列表(包括答案和解析)
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| n |
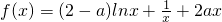 ;(a∈R).
;(a∈R).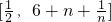 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由. ;(a∈R).
;(a∈R). 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.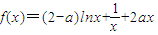 ;(a∈R).
;(a∈R).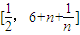 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.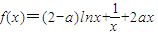 ;(a∈R).
;(a∈R).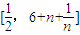 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.一、选择题
CBCDC BBDDD
二、填空题
11、-6 12、 13、5 14、[1,3
] (2分) [2,5] 15、4
13、5 14、[1,3
] (2分) [2,5] 15、4
16、⑴



三、解答题
17、⑴甲从选择题中抽到一题的可能结果有 个,乙从判断题中抽到一题的可能结果有
个,乙从判断题中抽到一题的可能结果有 个,故甲抽到选择题,乙抽到判断题的可能结果有
个,故甲抽到选择题,乙抽到判断题的可能结果有
 个,又甲、乙依次抽一题的可能结果有
个,又甲、乙依次抽一题的可能结果有 个,所以甲抽到选择题、乙抽到判断题的概率为:
个,所以甲抽到选择题、乙抽到判断题的概率为: (6分)
(6分)
⑵甲、乙二人依次都抽到判断题的概率为 ,故甲、乙二人中至少有一个抽到选择题的概率为
,故甲、乙二人中至少有一个抽到选择题的概率为
或用以下解法:
|