
题目列表(包括答案和解析)
(本小题满分12分)
一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4, ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
|
摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
|
“和为7”出现的频数 |
1 |
9 |
14 |
24 |
26 |
37 |
58 |
82 |
109 |
150 |
|
“和为7”出现的频率 |
0.10 |
0.45 |
0.47 |
0.40 |
0.29 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
(参考数据: )
)
(Ⅰ)如果试验继续下去,根据上表数据,出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率,并求 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,设定一种游戏规则:每次摸2球,若数字和为7,则可获得奖金7元,否则需交5元。某人摸球3次,设其获利金额为随机变量 元,求
元,求 的数学期望和方差。
的数学期望和方差。
(本小题满分12分)
一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4, ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
| “和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
 )
) 的值;
的值;  元,求
元,求 的数学期望和方差。
的数学期望和方差。(本小题满分12分)探究函数 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
16 |
10 |
8.34 |
8.1 |
8.01 |
8 |
8.01 |
8.04 |
8.08 |
8.6 |
10 |
11.6 |
15.14 |
… |
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数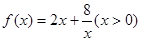 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数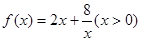 在区间 上递增.当
在区间 上递增.当 时,
时, .
.
(2)证明:函数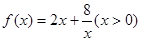 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考:函数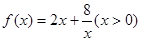 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(本小题满分12分)探究函数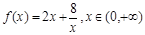 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
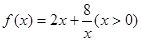 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数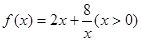 在区间 上递增.当
在区间 上递增.当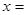 时,
时,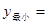 .
.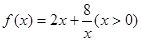 在区间(0,2)递减.
在区间(0,2)递减.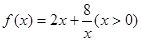 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)(本题满分12分)下表是某小卖部6天卖出热茶的杯数与当天气温的对比表:
|
气温/℃ |
26 |
18 |
13 |
10 |
4 |
-1 |
|
杯数 |
20 |
24 |
34 |
38 |
50 |
64 |
(Ⅰ)将上表中的数据制成散点图,并判断散点图中温度与饮料杯数是否成线性相关关系?
(Ⅱ)如果把上述关系近似成线性关系的话,经计算得回归方程 = bx+ a的系数 b= -1.65,请求出回归直线方程来近似地表示这种线性关系.(a的值精确到0.1)
= bx+ a的系数 b= -1.65,请求出回归直线方程来近似地表示这种线性关系.(a的值精确到0.1)
(Ⅲ)如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
一、选择题:1~12(5×12=60)
题号
01
02
03
04
05
06
07
08
09
10
11
12
答案
B
A
B
C
D
B
D
C
B
C
C
D
二、填空题:13、B.files\image063.gif) ;14、-
;14、-.files\image065.gif) ;15、32005;16、(2
;15、32005;16、(2.files\image063.gif) -2,2)。
-2,2)。
三、解答题:
17.解:(1)根据已知条件得:△=16sin2θ-4atanθ=0
即:a=.files\image068.gif) 2sin2θ 2分
2sin2θ 2分
又由已知:.files\image070.gif)
得.files\image072.gif) 4分
4分
所以有0<sin2θ<1
所以a∈(0,2) 6分
(2)当a=.files\image074.gif) 时由(1)得2sin2θ=
时由(1)得2sin2θ=.files\image074.gif) 8分
8分
所以sinθ=.files\image076.gif) ,而sin2θ=-cos(
,而sin2θ=-cos(.files\image078.gif) +2θ)
+2θ)
=-2cos2(.files\image080.gif) )+1=
)+1=.files\image076.gif) 10分
10分
所以cos2(.files\image080.gif) )=
)=.files\image083.gif) ,又
,又.files\image085.gif)
所以cos(.files\image080.gif) )=-
)=-.files\image087.gif) 12分
12分
18.解:(1)f′(x)=6x2-6(a+1)x+
∵函数f(x)在x=3处取得极值
∴x=3时,f′(x)=0
∴a=3 5分
(2)f′(x)=6(x-1)(x-a)
i)当a=1时,f′(x)≥0恒成立
函数f(x)在(-∞,+∞)上单调增 7分
ii)当a<1时,由f′(x)>0得x<1或x>a
∴单调增区间为(-∞,1),(a,+∞) 9分
iii)当a>1时,由f′(x)>0得x<1或x>a
∴单调增区间为(-∞,1),(a,+∞) 11分
综上:当a=1时,函数f(x)的增区间为(-∞,+∞)
当a<1时,函数f(x)的增区间为
(-∞,1),(1,+∞)
当a>1时,函数f(x)的增区间为
(-∞,1),(a,+∞) 12分
19.(九A解法)解:(1)取AC、CC1中点分别为M、N,连接MN、NB1、MB1,
∵AC1∥MN,NB1∥CE
∴∠MNB1是CE与AC1成角的补角 2分
Rt△NB.files\image089.gif)
Rt△MNC中,MN=6.files\image091.gif)
Rt△MBB1中,MB1=.files\image093.gif)
∴cos∠MNB1=-.files\image095.gif)
∴CE与AC1的夹角为arccos.files\image095.gif) 4分
4分
(2)过D作DP∥AC交BC于P,则A1D在面BCC1B1上的射影为C1P,而CE⊥A1D,由三垂线定理的逆定理可得CE⊥C1P,又BCC1B为正方形
∴P为BC中点,D为AB中点, 6分
∴CD⊥AB,CD⊥AA1
∴CD⊥面ABB
(3)由(2)CD⊥面A1DE
∴过D作DF⊥A1E于F,连接CF
由三垂线定理可知CF⊥A1E
∴∠CFD为二面角C-A1E-D的平面角 10分
又∵A1D=.files\image098.gif)
∴A1D2+DE2=A1E2=324
∴∠A1DE=90°
∴DF=6.files\image091.gif) ,又CD=6
,又CD=6.files\image091.gif)
∴tan∠CFD=1
∴∠CFD=45°
∴二面角C-A1E-D的大小为45° 12分
(此题也可通过建立空间直角坐标系,运用向量的方法求解)
20.解:由已知得:
不等式x2+px-4x-p+3>0,在p∈[0,4]上恒成立
即:p(x-1)+x2-4x+3>0,在p∈[0,4]上恒成立
令f(p)=p(x-1)+x2-4x+3
则有函数f(p)在p∈[0,4]上大于零恒成立。 4分
(1)显然当x=1时不恒成立
(2)当x≠1时,有.files\image102.gif) 即x>3或x<-1 10分
即x>3或x<-1 10分
所以x∈(3+∞)U(-∞,-1)为所求 12分
21.解:(1)经观察得第一行有20个数,第二行有21个数,第三行有22个数,第四行有23个数------
因此前n行有20+21+22+23+---+2n-1=.files\image104.gif) 个数
个数
所以,第n行的最后一个数是2n-1 4分
(2)由(1)知,前n-1行菜有2n-1-1个数,因此,第n行的第一个数为2n-1,第n行的最后一个是2n-1,它们构成公差为1的等差数列。
因此,由等差数列前n项和公式有:
.files\image106.gif) 8分
8分
(3)因为210=1024
211=2048
210<2008<211
所以2008位于第11行
该行第一个数是210=1024,由2008-1024+1=985
所以2008是第11和的985个数 。 12分
22.解:(1)由已知可设F(c,0),Q(x1,y1)
则.files\image108.gif)
∵.files\image110.gif)
∴c(x1-c)=1
∴x1=.files\image112.gif) 2分
2分
又直线FQ的方程为:y=tanθ(x-c)
∴y1=.files\image114.gif)
而S=.files\image116.gif)
=.files\image118.gif)
=.files\image120.gif) tanθ 4分
tanθ 4分
又已知.files\image120.gif) <S<2
<S<2
∴ .files\image120.gif) tanθ<4
tanθ<4
又θ为锐角
∴.files\image123.gif) <arctan4 7分
<arctan4 7分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com