练习册

  • 练习册
  • 试题
    13．(理)若实数满足.则的最大值为 . 【查看更多】

     

    题目列表(包括答案和解析)

    （理）若实数x，y满足则S = 2x+y的最大值为                                      （    ）

     

    A．7                               B．4                        C．3                        D．2

     

    查看答案和解析>>

    （08年西工大附中理）若实数x,y满足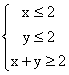，则x+2y的最小值和最大值分别为（   ）

    A．2，6         B．2，5        C．3，6       D．3，5

    查看答案和解析>>

    （08年华师一附中二次压轴理）已知实数x，y满足条件，若z=|x+2y+m|的最大值为21，则常数m的值为________________

    查看答案和解析>>

    已知数列是各项均不为0的等差数列，公差为d，为其前n项和，且满足,．数列满足,，为数列的前n项和．

    （1）求数列的通项公式和数列的前n项和；

    （2）若对任意的，不等式恒成立，求实数的取值范围；

    （3）是否存在正整数，使得成等比数列？若存在，求出所有的值；若不存在，请说明理由．

    【解析】第一问利用在中，令n=1，n=2，

    得   即      

    解得，， [

    又时，满足，

    ，

    第二问，①当n为偶数时，要使不等式恒成立，即需不等式恒成立．   

     ，等号在n=2时取得．

    此时 需满足．  

    ②当n为奇数时，要使不等式恒成立，即需不等式恒成立．     

     是随n的增大而增大， n=1时取得最小值-6．

    此时 需满足．

    第三问，

         若成等比数列，则，

    即．

    由，可得，即，

            ．

    （1）（法一）在中，令n=1，n=2，

    得   即      

    解得，， [

    又时，满足，

    ，

    ．

    （2）①当n为偶数时，要使不等式恒成立，即需不等式恒成立．   

     ，等号在n=2时取得．

    此时 需满足．  

    ②当n为奇数时，要使不等式恒成立，即需不等式恒成立．     

     是随n的增大而增大， n=1时取得最小值-6．

    此时 需满足．

    综合①、②可得的取值范围是．

    （3），

         若成等比数列，则，

    即．

    由，可得，即，

    ．

    又，且m>1，所以m=2，此时n=12．

    因此，当且仅当m=2， n=12时，数列中的成等比数列

     

    查看答案和解析>>

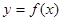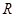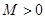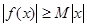    函数的定义域为，若存在常数，使得对一切实数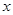均成立，则称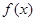为“圆锥托底型”函数．
    （1）判断函数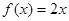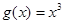，是否为“圆锥托底型”函数？并说明理由．
    （2）若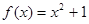是“圆锥托底型” 函数，求出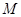的最大值．
    （3）问实数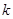、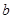满足什么条件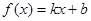，是“圆锥托底型” 函数．

    查看答案和解析>>

    1．解析：，故选A。

    2．（理）解析：∵

    ，

    故选B。

    （文）解析：抽取回族学生人数是，故选B。

    3．解析：由，得，此时，所以，，故选C。

    4．（理）解析：显然，若与共线，则与共线；若与共线，则，即，得，∴与共线，∴与共线是与共线的充要条件，故选C。

    （文）解析：∵∥，∴，∴，故选C。

    5．解析：设公差为，由题意得，；，解得或，故选C。

    6．解析：（理）∵双曲线的右焦点到一条渐近线的距离等于焦距的，∴，又∵，∴，∴，∴双曲线的离心率是。故选B.

    （文）∵双曲线的右焦点到一条渐近线的距离等于焦距的，∴，又∵，∴，∴双曲线的渐近线方程是,故选D.

    7.解析：∵、为正实数，∴，∴；由均值不等式得恒成立，，故②不恒成立，又因为函数在是增函数，∴，故恒成立的不等式是①③④。故选C.

    8．解析：∵，∴在区间上恒成立，即在区间上恒成立，∴，故选D。

    9．（理）解析：∵

    ，此函数的最小值为，故选C。

    （文）解析：∵

    ，∴此函数的最小正周期是，故选C。

    10．解析：如图，∵正三角形的边长为，∴，∴，又∵，∴，故选D。

    11．解析：∵在区间上是增函数且，∴其反函数在区间上是增函数，∴，故选A

    12．解析：如图，①当或时，圆面被分成2块，涂色方法有20种；②当或时，圆面被分成3块，涂色方法有60种；

    ③当时，圆面被分成4块，涂色方法有120种，所以m的取值范围是，故选A。

    13．（理）解析：做出表示的平面区域如图，当直线经过点时，取得最大值5。

    （文）解析：将代入结果为，∴时，表示直线右侧区域，反之，若表示直线右侧区域，则，∴是充分不必要条件。

    14.解析：（理）∵，∴时，，又时，满足上式，因此，，

    ∴。

    学科网(Zxxk.Com) （文）∵，∴时，，又时，满足上式，因此，。

    学科网(Zxxk.Com)15．解析：设正四面体的棱长为，连，取的中点，连，∵为的中点，∴∥，∴或其补角为与所成角，∵，，∴，∴，又∵，∴，∴与所成角的余弦值为。

    学科网(Zxxk.Com)16．解析：∵，∴，∵点为的准线与轴的交点，由向量的加法法则及抛物线的对称性可知，点为抛物线上关于轴对称的两点且做出图形如右图，其中为点到准线的距离，四边形为菱形，∴，∴，∴，∴，∴，∴向量与的夹角为。

    17．(10分)解析：（Ⅰ）由正弦定理得，，，…2分

    ∴，，………4分

    （Ⅱ）∵，，∴，∴，………………………6分

    又∵，∴，∴，………………………8分

    ∴。………………………10分

    18.解析：（Ⅰ）∵，∴；……………………理3文4分

    （Ⅱ）∵三科会考不合格的概率均为，∴学生甲不能拿到高中毕业证的概率；……………………理6文8分

    （Ⅲ）∵每科得A，B的概率分别为，∴学生甲被评为三好学生的概率为。……………………12分

    （理）∵，，，。……………………9分

    ∴的分布列如下表：

    0

    1

    2

    3

    ∴的数学期望。……………………12分

    19．(12分)（理）解析：（Ⅰ）时，

    ，，

        

    由得， 或   ………3分

     

     

    +

    0

    －

    0

    +

    递增

    极大值

    递减

    极小值

    递增

    ，      ………………………6分

    （Ⅱ）在定义域上是增函数，

    对恒成立，即              

       ………………………9分

    又（当且仅当时，）

                   

     ………………………4分

                  

    （文）解析：（Ⅰ）∵，∴，

     ，，………………………3分

    （Ⅱ）∵，∴，

    学科网(Zxxk.Com)∴，

    又，∴数列自第2项起是公比为的等比数列，………………………6分

    ∴，………………………8分

    （Ⅲ）∵，∴，………………………10分

    ∴。………………………12分

    20．解析：（Ⅰ）∵∥，，∴，∵底面，∴，∴平面，∴，又∵平面，∴，∴平面，∴。………………………4分

    （Ⅱ）∵平面，∴，，∴为二面角的平面角，………………………6分

    ，，∴，又∵平面，，∴，∴二面角的正切值的大小为。………………………8分

    （Ⅲ）过点做∥，交于点，∵平面，∴为

    同步练习册答案