如图,三棱锥中,侧面底面, ,且,.(Ⅰ)求证:平面;

(Ⅱ)若为侧棱PB的中点,求直线AE与底面所成角的正弦值.

【解析】第一问中，利用由知, ,

又AP=PC=2,所以AC=2,

又AB=4, BC=2,,所以,所以,即,

又平面平面ABC,平面平面ABC=AC, 平面ABC,

平面ACP,所以第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证平面ABC,又EH//PO,所以EH平面ABC ,

则为直线AE与底面ABC 所成角,

解

 (Ⅰ) 证明:由用由知, ,

又AP=PC=2,所以AC=2,

又AB=4, BC=2,,所以,所以,即,

又平面平面ABC,平面平面ABC=AC, 平面ABC,

平面ACP,所以

………………………………………………6分

(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,

因为PA=PC,所以PO⊥AC,同(Ⅰ)易证平面ABC,

又EH//PO,所以EH平面ABC ,

则为直线AE与底面ABC 所成角,

且………………………………………10分

又PO=1/2AC=,也所以有EH=1/2PO=,

由(Ⅰ)已证平面PBC,所以,即,

故,

于是

所以直线AE与底面ABC 所成角的正弦值为

填空题
【小题1】已知数列为等差数列，为其前项和         
【小题2】函数的反函数为，则    。
【小题3】已知球O的表面上四点A、B、C、D，平面ABC，ABBC，DA=AB=BC=，则球O的体积等于        。
【小题4】某校在2010年的“八校第一次联考”中有1000人参加考试，数学考试的成绩（，试卷满分150分），统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的，则此次数学考试成绩不低于110分的学生约有     人。
【小题5】有一种数学推理游戏，游戏规则如下：

①在9×9的九宫格子中，分成9个3×3的小九格，用1到9这9个数填满整个格子；
②每一行与每一列都有1到9的数字，每个小九宫格里也有1到9的数字，并且一个数字在每 行每列及每个小九宫格里只能出现一次，既不能重复也不能少，那么A处应填入的数字为          ；B处应填入的数字为       。

已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.

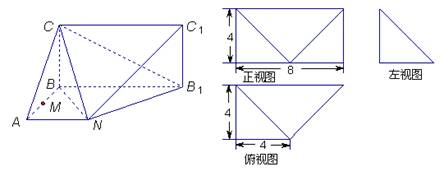
（1）证明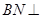：平面；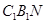

（2）求二面角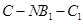的余弦值；

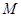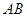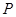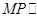（3）为的中点，在线段上是否存在一点，使得平面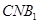，若存在，求出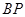的长;若不存在，请说明理由.

（本题满分14分）已知函数

（1）用五点法画出它在一个周期内的闭区间上的图象；

（2）指出的周期、振幅、初相、对称轴；

(3)说明此函数图象可由上的图象经怎样的变换得到