
题目列表(包括答案和解析)
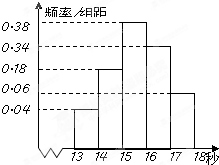 (2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.| 性别 是否 达标 |
男 | 女 | 合计 |
| 达标 | a=24 | b= 6 6 |
30 30 |
| 不达标 | c= 8 8 |
d=12 | 20 20 |
| 合计 | 32 32 |
18 18 |
n=50 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
(文)有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5.39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,数据落在[31.5,43.5)的概率约是( )
A.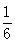 B.
B. C.
C.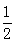 D.
D.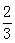
(文)有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5.39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,数据落在[31.5,43.5)的概率约是( )
A.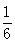 | B.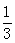 | C.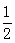 | D.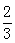 |
| 61分以下 | (61,70](分) | (71,80](分) | (81,90](分) | (91,100](分) | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 4 | 8 | 13 | 15 | 10 |
| 优秀人数 | 非优秀人数 | 总计 | |
| 甲班 | 30 30 |
20 20 |
50 50 |
| 乙班 | 25 25 |
25 25 |
50 50 |
| 总计 | 55 55 |
45 45 |
100 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com