
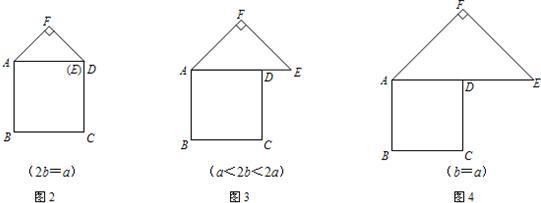
25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例:
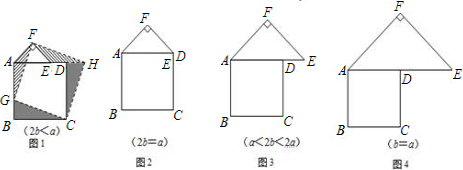
当2b<a时,如图1,在BA上选取点G,使BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现:
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连接CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究:
(1)正方形FGCH的面积是
a2+b2
;(用含a,b的式子表示)
(2)类比图1的剪拼方法,请你就图2-图4的三种情形分别画出剪拼成一个新正方形的示意图.
联想拓展:
小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移;当b>a时,如图5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.





 25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.

 有足够多的长方形和正方形卡片,如图:
有足够多的长方形和正方形卡片,如图:
