
题目列表(包括答案和解析)
| x+a |
| 3 |
| 2x-1 |
| 3 |
 问:该宾馆一天的最高客房收入能达到12 000元吗?若能,求出此时高级客房的价格;若不能,请说明理由.
问:该宾馆一天的最高客房收入能达到12 000元吗?若能,求出此时高级客房的价格;若不能,请说明理由.| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
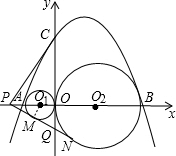 于点P、Q(M、N为切点,如图所示),求△CPQ的面积.
于点P、Q(M、N为切点,如图所示),求△CPQ的面积.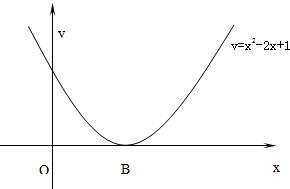 7、已知抛物线y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x+1的顶点是B.
7、已知抛物线y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x+1的顶点是B.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com